- (
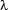 -)bound: 3.4.1 Lambda-Abstraction
-)bound: 3.4.1 Lambda-Abstraction
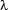 -abstraction: 3.4.1 Lambda-Abstraction
-abstraction: 3.4.1 Lambda-Abstraction
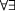 -constellation: 10.1.4 Rule-like World Knowledge and Computational Nightmares
-constellation: 10.1.4 Rule-like World Knowledge and Computational Nightmares
 -conversion: 3.4.8 Alpha-Conversion
-conversion: 3.4.8 Alpha-Conversion
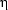 -equivalent: 5.2.10 Sidetrack: Predicates versus Functions
-equivalent: 5.2.10 Sidetrack: Predicates versus Functions
 -equivalent: 3.4.8 Alpha-Conversion
-equivalent: 3.4.8 Alpha-Conversion
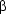 -reduction: 3.4.2 Reducing Complex Expressions
-reduction: 3.4.2 Reducing Complex Expressions
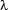 -structure: 5.2.6 Describing Lambda-Structures
-structure: 5.2.6 Describing Lambda-Structures
- abstracted over: 3.4.1 Lambda-Abstraction
- admissible: 10.7 Exercises
- anaphoric pronoun: 11.1.1 Anaphoric Pronouns
- antecedent: 7.1.3 A simple Logical System: Propositional Logic with Hilbert-Calculus
- argument type: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
- assumption: 7.1.2 Calculi
- atomic formula: 1.1.6 Building Formulae
- axiom: 7.1.3 A simple Logical System: Propositional Logic with Hilbert-Calculus
- axiomatic method: 7.1.4 Proofs in Hilbert Calculus
- binding edge: 5.2.5 Formulas are trees!, 5.2.6 Describing Lambda-Structures
- bound variable: 1.1.7 Subformulae, Free Variables
- Calculemus!: 7.1.6 Sidetrack: Calculemus!
- calculus: 7.1.2 Calculi
- calculus ratiocinator: 7.1.6 Sidetrack: Calculemus!
- chaining rule: 7.2.8 Sidetrack: Practical Enhancements for Tableaux
- characteristic function: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
- Choice Rule: 6.2.1 The Choice Rule
- closed: 7.2.1 Tableaux for Theorem Proving, 7.2.3 Analytical Tableaux: A more formal Account
- combinatorial explosion: 5.1.8 The Problem with the Traditional Approaches
- complete: 7.1.4 Proofs in Hilbert Calculus, 7.1.5 Properties of Calculi (Theoretical Logic)
- computation tree: 8.1.5 An Example - first Steps
- conclusion: 7.1.2 Calculi, 7.1.3 A simple Logical System: Propositional Logic with Hilbert-Calculus
- confluence: 3.4.3 Using Lambdas
- conjunctive expansion: 7.2.1 Tableaux for Theorem Proving
- constant symbol: 1.1.1 Vocabularies
- constraint graph: 5.2.6 Describing Lambda-Structures
- constraint solving: 5.2.4 The Masterplan, 5.2.3 Underspecified Descriptions
- contradiction-free: 9.1.3 Tableaux Branches and Herbrand Models
- conversational implicature: 7.2.5 An Application: Conversational Maxims
- conversational maxim: 7.2.5 An Application: Conversational Maxims
- cooperative principle: 7.2.5 An Application: Conversational Maxims
- Cooper storage: 5.1.7 Other Traditional Solutions
- correct: 7.1.5 Properties of Calculi (Theoretical Logic), 7.1.4 Proofs in Hilbert Calculus
- d-compositionality: 3.1.3 [Sidetrack] Compositional Semantics
- decision procedure: 9.1.4 Tableaux generate Herbrand Models
- deduction theorem: 1.2.7 An Example
- derivability: 7.1.4 Proofs in Hilbert Calculus
- derived rule: 7.2.8 Sidetrack: Practical Enhancements for Tableaux
- describe: 5.2.8 Relating Constraint Graphs and Lambda-Structures
- discourse: 9.1.4 Tableaux generate Herbrand Models, 10.7 Exercises
- discourse referent: 11.2.1 A First Example
- Discourse Representation Structure (DRS): 11.1.3 Another Puzzle
- Discourse Representation Theory (DRT): 11.1.3 Another Puzzle
- disjunctive: 7.2.2 Tableaux for Theorem Proving (continued)
- Distribution Rule: 6.2.1 The Choice Rule
- domain: 1.1.2 First-Order Models
- dominance edge: 5.2.6 Describing Lambda-Structures
- donkey sentence: 11.1.2 Donkey Sentences
- Enumeration: 6.1.1 Satisfiability and Enumeration
- exact model: 1.1.3 An Example Model, 1.1.4 Exact Models
- existential: 10.5 Sidetrack: Derived Rules for the Existential Quantifier
- fairness: 10.2.6 Subsequent Instantiations: Instantiate
- finite model property: 9.1.4 Tableaux generate Herbrand Models
- first-order formula: 1.1.5 First-Order Languages
- first-order language: 1.1.5 First-Order Languages
- first-order model: 1.1.2 First-Order Models, 1.1.2 First-Order Models, 1.1.1 Vocabularies
- first order tableaux: 1.2.6 Valid Arguments
- free variable: 1.1.7 Subformulae, Free Variables
- functional application: 3.4.2 Reducing Complex Expressions
- Herbrand base: 10.1.2 Extending our Calculus: The Universal Rule
- Herbrand model: 9.1.3 Tableaux Branches and Herbrand Models
- inference: 6.6 Exercises, Course Schedule
- inference system: 7.1.2 Calculi
- initial tableaux: 7.2.3 Analytical Tableaux: A more formal Account
- instance: 7.1.4 Proofs in Hilbert Calculus
- interpretation: 1.2.2 Interpretations and Variant Assignments
- interpretation function: 1.1.2 First-Order Models
- iterative-deepening: 10.2.3 Restricting the Application of the Universal Rule
- Keller storage: 5.1.7 Other Traditional Solutions
- lexical semantic: 9.1.1 Why Model Generation?
- lingua universalis: 7.1.6 Sidetrack: Calculemus!
- literal: 1.1.6 Building Formulae
- logical constant: 10.6 Project: Adding Equality to our Calculus
- Manner: 7.2.5 An Application: Conversational Maxims
- matrix: 1.1.6 Building Formulae
- meaning construction: Course Schedule
- mental model: 9.1.1 Why Model Generation?
- model generation: 9 [Sidetrack] Model Generation
- model generation procedure: 9.1.2 Tableaux for Model Generation with PLNQ
- modus ponens: 7.1.3 A simple Logical System: Propositional Logic with Hilbert-Calculus
- name: 1.1.1 Vocabularies
- negative: 7.2.3 Analytical Tableaux: A more formal Account
- Nested Cooper storage: 5.1.7 Other Traditional Solutions
- normal dominance constraint: 5.2.3 Underspecified Descriptions, 5.2.4 The Masterplan, 5.2.9 Sidetrack: Constraint Graphs - The True Story
- normalization: 6.2.2 Normalization
- normal model: 1.3.2 Semantics of Equality
- open: 7.2.3 Analytical Tableaux: A more formal Account, 7.2.1 Tableaux for Theorem Proving
- parent normalization: 6.2.2 Normalization
- PLNQ: 7.2.4 Using Tableaux to test Truth Conditions
- predicate symbol: 1.1.1 Vocabularies
- premise: 7.1.3 A simple Logical System: Propositional Logic with Hilbert-Calculus
- proof: 7.1.2 Calculi, 7.1.4 Proofs in Hilbert Calculus
- proof from the assumptions in
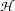 : 7.1.4 Proofs in Hilbert Calculus
: 7.1.4 Proofs in Hilbert Calculus
- proof theory: 1.2.6 Valid Arguments
- provability: 7.1.4 Proofs in Hilbert Calculus, 7.1.4 Proofs in Hilbert Calculus
- provable: 7.1.5 Properties of Calculi (Theoretical Logic), 7.1.4 Proofs in Hilbert Calculus, 7.1.5 Properties of Calculi (Theoretical Logic), 7.1.4 Proofs in Hilbert Calculus, 7.1.4 Proofs in Hilbert Calculus
- provable from the assumptions in
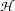 : 7.1.4 Proofs in Hilbert Calculus
: 7.1.4 Proofs in Hilbert Calculus
- Quality: 7.2.5 An Application: Conversational Maxims
- quantifier store: 5.1.7 Other Traditional Solutions
- quantifying in: 5.1.4 The Fifth Reading, 5.1.5 Montague's Approach to the Scope Problem
- Quantity: 7.2.5 An Application: Conversational Maxims
- redundancy elimination: 6.2.2 Normalization
- refutation proof: 7.2.3 Analytical Tableaux: A more formal Account
- Relation: 7.2.5 An Application: Conversational Maxims
- relation symbol: 1.1.1 Vocabularies
- result type: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
- s-compositionality: 3.1.3 [Sidetrack] Compositional Semantics
- Satisfiability: 6.1.1 Satisfiability and Enumeration
- saturated: 7.2.3 Analytical Tableaux: A more formal Account
- scope: 1.1.6 Building Formulae
- scope ambiguity: 5.1.1 What Are Scope Ambiguities?
- semi-decidable: Consequences for Theorem Proving
- sentence: 1.1.7 Subformulae, Free Variables
- signature: 1.1.1 Vocabularies
- signed: 7.2.3 Analytical Tableaux: A more formal Account, 7.2.1 Tableaux for Theorem Proving
- simply typed
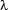 -calculus: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
-calculus: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
- skolem constant: 10.1.3 The Existential Rule
- solution: 5.2.8 Relating Constraint Graphs and Lambda-Structures
- solved form: 6.1.4 Defining Solved Forms
- sound: 7.1.5 Properties of Calculi (Theoretical Logic), 7.1.4 Proofs in Hilbert Calculus
- specification: 2.1.4 Representing Models
- subformula: 1.1.7 Subformulae, Free Variables
- subordination: 11.2.3 Syntax of DRSs and DRS-Conditions
- succedent: 7.1.3 A simple Logical System: Propositional Logic with Hilbert-Calculus
- syncategorematically: 4.4.2 The Lexicon, 4.4.3 ``Special'' Words
- syntactic structure: 3.1.2 Being Systematic (II)
- tableaux proof: 7.2.3 Analytical Tableaux: A more formal Account
- tableaux refutation: 7.2.3 Analytical Tableaux: A more formal Account
- term: 1.1.6 Building Formulae
- test calculus: 7.2.3 Analytical Tableaux: A more formal Account
- theorem: 7.1.4 Proofs in Hilbert Calculus
- true in a model: 1.2.3 The Satisfaction Definition, 1.2.4 Truth in a Model
- universal: 10.5 Sidetrack: Derived Rules for the Existential Quantifier
- valid: 7.1.5 Properties of Calculi (Theoretical Logic), 7.1.5 Properties of Calculi (Theoretical Logic), 7.1.4 Proofs in Hilbert Calculus, 7.1.4 Proofs in Hilbert Calculus
- valid argument: 1.2.6 Valid Arguments
- valid formula: 1.2.5 Validities
- validity: 7.1.4 Proofs in Hilbert Calculus
- valid sentence: 1.2.5 Validities
- variant: 1.2.2 Interpretations and Variant Assignments
- vocabulary: 1.1.1 Vocabularies
- well-formed formula: 1.1.6 Building Formulae
- well-typed: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
- witness: 10.1.3 The Existential Rule
- world knowledge: 9.3 Wrapping it up (Model Generation)
- x-variant: 1.2.2 Interpretations and Variant Assignments
Aljoscha Burchardt, Stephan Walter, Alexander Koller, Michael Kohlhase, Patrick Blackburn and Johan Bos
Version 1.2.5 (20030212)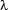 -)bound: 3.4.1 Lambda-Abstraction
-)bound: 3.4.1 Lambda-Abstraction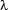 -)bound: 3.4.1 Lambda-Abstraction
-)bound: 3.4.1 Lambda-Abstraction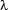 -abstraction: 3.4.1 Lambda-Abstraction
-abstraction: 3.4.1 Lambda-Abstraction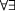 -constellation: 10.1.4 Rule-like World Knowledge and Computational Nightmares
-constellation: 10.1.4 Rule-like World Knowledge and Computational Nightmares -conversion: 3.4.8 Alpha-Conversion
-conversion: 3.4.8 Alpha-Conversion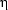 -equivalent: 5.2.10 Sidetrack: Predicates versus Functions
-equivalent: 5.2.10 Sidetrack: Predicates versus Functions -equivalent: 3.4.8 Alpha-Conversion
-equivalent: 3.4.8 Alpha-Conversion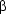 -reduction: 3.4.2 Reducing Complex Expressions
-reduction: 3.4.2 Reducing Complex Expressions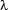 -structure: 5.2.6 Describing Lambda-Structures
-structure: 5.2.6 Describing Lambda-Structures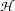 : 7.1.4 Proofs in Hilbert Calculus
: 7.1.4 Proofs in Hilbert Calculus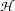 : 7.1.4 Proofs in Hilbert Calculus
: 7.1.4 Proofs in Hilbert Calculus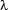 -calculus: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus
-calculus: 3.4.4 [Sidetrack] Simply Typed Lambda-Calculus