7.1.2 Calculi

Motivation of calculi.

From a theoretical perspective, talking about models (as we did it in Chapter 1) enables us to define neatly e.g. which sentences follow from a particular sentence. But from a computational perspective, using models to actually compute what follows from a sentence is impossible. First of all, models may be infinite. But even if we restrict ourselves to using finite models, the fact that the semantic notion of logical consequence (as well as that of validity) is defined with respect to all models makes computation intractable.

Assumptions, Inference, Conclusions

Therefore, logics typically have a third part, an inference system (also called a calculus ), which is a syntactic counterpart to the semantic notions. By saying that it is syntactic, we mean that such a system works without recourse to meaning, by considering only the syntactic structure of formulae. Hence a calculus gives us the syntactic counterpart to the semantic concept of logical consequence. Formally, a calculus is a set of rules that transform (sets of) formulae into other (sets of) formulae. The formulae given as input are called assumption s, the resulting formulae are called conclusion s. In what follows, we will use a tableaux calculus to infer what formulae follow from some given other ones.

Proof

But before that, let us look at the syntactic counterpart of validity. A sequence of rule applications that transform the empty set of assumptions into a formula 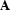, is called a proof of 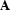. To make this clear, let us turn to a very simple example.