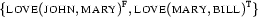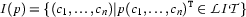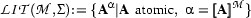9.1.3 Tableaux Branches and Herbrand Models

Relation between tableaux and models.

In this section we explore the relation between literals on saturated branches and models in more detail. Put in more professional terms, there's one general property of tableaux calculi of which we take advantage in model generation: The set of literals on an open saturated tableaux branch corresponds to a Herbrand model for the input formula of the tableaux.

A Second Look at our Example

To fortify our intuition, we will study our example above, where the set of literals on the open branch is

and build such a model.

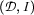Let us recap: A Herbrand model is a model (a pair of a domain and an interpretation function) where individual constants are interpreted "as themselves". Our formula mentions ``Mary'', ``John'', and ``Bill'', so let us take 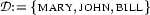and fix , , .

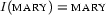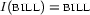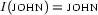So the remaining task is to find a suitable interpretation for the predicate 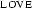that makes 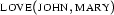false and 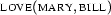true. This is simple: we just take 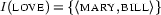. Indeed we then have 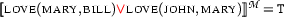and 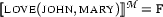according to the definition of the interpretation function.

More Formally

Now let us generalize what we have just done for our example to arbitrary sets of literals coming from a saturated open tableaux branch. Let be such a set of literals. Note that 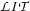necessarily is contradiction-free : It cannot contain literals 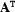and 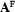at the same time; otherwise the branch would be closed.

Fixing the Domain

We take the domain of interpretation to be isomorphic to the set 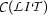of individual constants occurring in 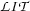. The simplest thing to achieve this isomorphism, is just to take 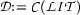and take to be the identity function on individual constants 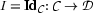. This means that all constant symbols will simply denote themselves. Note that choosing 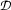this way is the most general possibility as long as we assume all individuals to be distinct. If we wanted to be able to express equality between induividuals (say between Mary and Bill, in which case we would know that he/she loves him/herself), we would have to add more structure to our domain, shifting to normal models.

Herbrand models

Now we can give a formal definition of Herbrand models. We will call a model a Herbrand model , iff 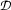is a set 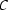of individual constants and is the identity on .

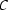Interpreting Predicates

The only thing still to be done now is fixing the interpretation of predicates so that they satisfy the literals in 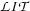. Again, we make the choice that commits us least. So we choose the extension of our predicates that makes exactly the positive literals in 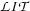true. That is we take

for every -ary predicate that occurs in 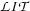. Note that 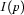is well-defined, since 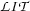does not contain contradictions. In result, each predicate will be interpreted as the set of those tuples of constant symbols that appear as arguments in positive literals for the respective predicate in .

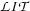What have we achieved?

Now we have fully specified a model 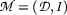, such that 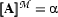for each 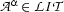. In other words, we have found a model that satisfies all literals in .

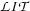On the other hand, for any model 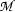, the set

of literals is contradiction-free, since 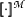is a function. So contradiction-free sets of literals are representations of models. Note that this is why we sloppily say that some set of literals is a (Herbrand) model. If this sounds familiar, that's no wonder. We have done the same argumentation when we had to represent models in Prolog.