10.6 Project: Adding Equality to our Calculus

We will explain how to extend our tableaux calculus by equality, which is a very important relation in natural language. Your project will be to extend our implementation accordingly.

logical constant

Generally, extending a logic with a new logical constant - equality is counted as a logical constant , since its semantics is fixed in all models - involves extending all three components of the logical system: the language, semantics, and the calculus.

Two new rules

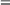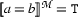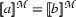We have already considered the logical ramifications of this extension in Section 1.3 (we have just added a binary relation to the vocabulary, and , iff ). Thus we can concentrate on the calculus side here: We add two inference rules (a positive and a negative) for the new principal constant.

An example

The following example shows how the second of the two rules works: If we simplify the translation of definite noun phrases, so that the phrase ``the teacher'' translates to a concrete individual constant 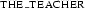(of course one could think of more principled ways to treat definite noun phrases), then we can interpret (1) as (2).

1. ``Mary is the teacher. Peter likes the teacher''.

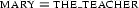2. and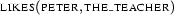

Thus interpreting (1) leads to the following model generation tableau:

In particular, we can test whether our two sentences entail that ``Peter likes Mary'' using the method from the last section: the tableaux

confirms our intuition that Peter likes her.

A new closure rule

There's one small complication: An equality statement can be contradictory in itself. For example, there can be no model already for the literal 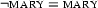(respectively 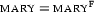) alone. Thus we must close a tableaux branch on such a statement (and obviously we don't have to find a ``partner'' for it, like normally when we look for contradictions). This is captured in the following rule:

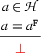
The project

Extend our implementation of first-order tableaux to include a treatment of equality as just discussed. [Hint: First of all you will of course have to decide what symbol to use for equality. You shouldn't use = or == for this purpose, because both already have a meaning in Prolog. You can e.g. use === or eq instead.]