7.2.2 Tableaux for Theorem Proving (continued)
Continuation.
Disjunctive Expansion
We continue our tableaux construction by expanding the formula 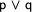 . Under what conditions is this formula true? There are two possibilities: Either
. Under what conditions is this formula true? There are two possibilities: Either 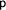 is true or
is true or 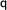 is true. We express this in a tableaux by introducing a branching (we call this a disjunctive expansion):
is true. We express this in a tableaux by introducing a branching (we call this a disjunctive expansion):
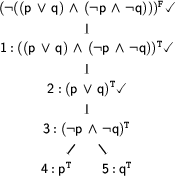
On each new branch, we pursue one of the possibilities to make the decomposed formula true. Now there is only one complex formula left to be expanded: 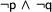 . This expansion is like the second expansion again: The formula is true if both subformulae are true. So, we add these formulae conjunctively again.
. This expansion is like the second expansion again: The formula is true if both subformulae are true. So, we add these formulae conjunctively again.
To which branch should we add the new formulae? The answer is: to both. The expanded formula occurs on both branches and so both should get to see the result.
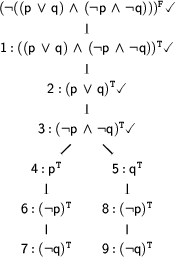
This time there are four expansions we could apply next: We could expand node 6 or 7 on the left branch, or node 8 or 9 on the right one. We could in principle choose any of them. But remember that we want to have a closed tableaux, i.e. we want each branch to be closed. So it's a good idea to expand the nodes 6 and 9 next. The expansion of node 6 gives us  on the left branch and the expansion of node 9 gives us
on the left branch and the expansion of node 9 gives us 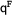 on the right branch. These two expansions give us a closed tableaux (we indicate closed branches by a
on the right branch. These two expansions give us a closed tableaux (we indicate closed branches by a  )!
)!
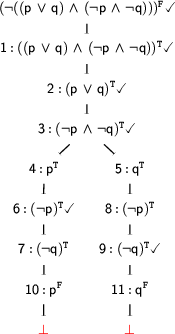
Signed Branch Closure
We call a branch closed iff there are two occurrences of the same atom with different signs on this branch (like 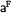 and
and 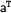 ). So, we are done: We have generated a tableaux proof for the theorem
). So, we are done: We have generated a tableaux proof for the theorem 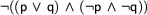 !
!
Exercise 7.1
Add annotations to the nodes of the tableaux above. The annotations should indicate from where each node resulted, and why. For example, node 1 would be annotated "from Input", and node 2 something like "from 1, making a conjunction true". Additionally, the closure nodes (
) should be annotated with the numbers of the respective contradictory nodes.