7.1.4 Proofs in Hilbert Calculus
Continuation.
Proof
An occurence of a rule schema where all schematic formulae (like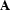 
, 
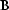etc.) have been replaced by actual formulae of the language is called an instance of that schema. A proof with our little calculus is simply a sequence of instances of the inference rule schema, such that the antecedents of each rule are succedents of rules earlier in the sequence. If we additionally allow formulae from a set 
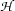into the sequence, we speak of a proof from the assumptions in 
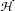. Any formula that occurs in a proof generated from our Hilbert calculus is provable (or provable from the assumptions in 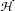if it occurs in a proof from these assumptions). So intuitively, if we want to prove a formula, we take a (possibly empty) set of assumptions and apply the inference rules until we have produced our formula as the conclusion of some rule application.
Theorem
We will write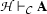 
if the formula 
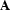is provable from the assumptions in 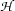in the calculus 
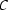. We will call the relation 
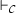the derivability or provability relation for .
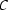We will simply write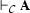 
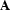if is provable from the assumptions in 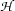(so 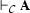a shorthand for 
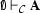). A formula that is provable without any further assumptions is called a theorem .
An Example Proof
Let us look at an example to fortify our intuition. We will prove the theorem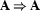 
.
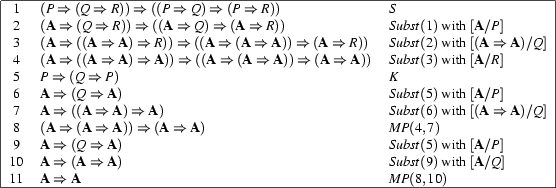
There are two things to note about this proof.
The inference rules can be applied in a purely schematic and syntactic fashion. It does not play a role what the formulae that are manipulated actually mean.
The actual proof proof is long, tedious, and in this particular case very un-intuitive.
The last observation is negative. But it mainly has to do with the particular calculus we're using. We will discuss a more intuitive calculus (called semantic tableaux) later.
The Axiomatic Method
The first observation in contrast is a positive one. Indeed it is the great pro of using calculi (or the axiomatic method , as one also says): Instead of thinking about infinitely many models for validity , we can consider provability , which can be exhibited by pure syntactic formula manipulation. The only question that remains is how provability and validity relate to each other. In other words: We want to justify our calculus in terms of semantics again.