1.1.5 First-Order Languages

Introduction of the concept of a first-order language.

We now understand what a vocabulary is, and we've learned about models, the semantic entities corresponding to vocabularies. It's time now to turn to the notion of first-order formula e. First-order formulae are derived from first-order languages. And a first-order language defines how we can use a vocabulary to form complex, sentence-like entities. Starting from a vocabulary, we then build the first-order language over that vocabulary out of the following ingredients:

The Ingredients.

1. All of the symbols in the vocabulary. We call these symbols the non-logical symbols of the language.

2. A countably infinite collection of variables 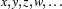, and so on.

3. The Boolean connectives (negation), 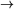(implication), 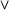(disjunction), and 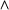(conjunction).

4. The quantifiers 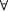(the universal quantifier) and 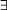(the existential quantifier).

5. The round brackets ) and (. (These are essentially punctuation marks; they are used to group symbols.)

Items 2-5 are common to all first-order languages: the only aspect that distinguishes first-order languages from one another is the choice of non-logical symbols (that is, of vocabulary).