3.4.8 Alpha-Conversion
-conversion helps avoid accidental bindings.
But such interactions need never happen. Obviously at the heart of our problem lies the fact that we used two variables named 
in our representation. But 
-bound variables are merely placeholders for substitution slots. The exact names of these placeholders do not play a role for their function. So, relabeling bound variables yields -expressions which lead to exactly the same substitutions in terms of 'slots in the formulas' (much like relabeling bound variables in quantified formulas doesn't change their truth values).
Let us look at an example. The -expressions 
, 
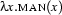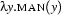, and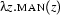 
are equivalent, as are the expressions 
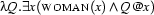and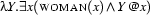 
. All these expressions are functors which when applied to an argument, replace the bound variable by the argument. No matter which argument 
we choose, the result of applying any of the first three expressions to and then 
-converting is 
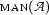, and the result of applying either of the last two expressions to is 
.
-Equivalence
Two -expressions are called -equivalent if they only differ in the names of -bound variables. In what follows we often treat -equivalent expressions as if they were identical. For example, we will sometimes say that the lexical entry for some word is a -expression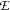 
, but when we actually work out some semantic construction, we might use an -equivalent expression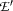 
instead of 
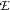itself.
-Conversion
The process of relabeling bound variables is called -conversion . Since the result of -converting an expression performs the same task as the initial expression, -conversion is always permissible during semantic construction. But the reader needs to understand that it's not merely permissible to -convert, it can be vital to do so if 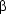-conversion is to work as intended.
Returning to our intial problem, if we can't use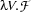 
as a functor, any -equivalent formula will do instead. By suitably relabeling the bound variables in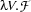 
we can always obtain an -equivalent functor that doesn't bind any of the variables that occur free in 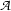, and accidental binding is prevented.
So, strictly speaking, it is not merely functional application coupled with 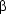-conversion that drives the process of semantic construction in this course, but functional application and 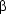-conversion coupled with (often tacit) use of -conversion. Notice we only didn't encounter the problem of accidental binding earlier because we (tacitly) chose the names for the variables in the lexical representations cleverly. This means that we have been working with -equivalent variants of lexical entries all along in our examples.