1.1.2 First-Order Models

Definition of the concept of a first-order model .

Let's suppose we've established a vocabulary. What would a first-order model for this vocabulary be?

If you read it again thoroughly, our previous discussion pretty much contains the answer to this: Intuitively, a model is a situation. A situation is a semantic entity, providing us with a certain amount of things we can talk about. Thus, a model for a given vocabulary gives us two pieces of information. First, it tells us what kind of collection of entities (usually called the domain , or 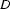for short) we can talk about. Secondly, for each symbol in the vocabulary, it gives us an appropriate semantic entity, built from the items in 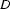, this task being carried out by a function which, for each symbol in the vocabulary, specifies an appropriate semantic value. A function like this is what we call interpretation function .

What is a Model?

Thus, in set theoretic terms, a model 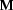is an ordered pair 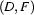composed of a domain 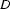and an interpretation function specifying semantic values in .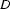

What are appropriate semantic values? There's no mystery here. Since constants are names, each constant should be interpreted as an element of 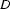. (That is, for each constant symbol in the vocabulary, 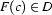.) Since -place relation symbols denote -place relations, each -place relation symbol should be interpreted as an -place relation on 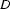. (That is, 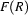should be a set of -tuples of elements of 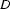.)