1.2.2 Interpretations and Variant Assignments
Let's suppose we've fixed our vocabulary. (Note: Whenever we talk of a model
from now on, we mean a model of this vocabulary, and whenever we talk of formulae, we mean the formulae built from the symbols in that vocabulary.) We now give two further technical definitions which will enable us to state the satisfaction definition in a concise manner.
Let's suppose we've fixed our vocabulary. (Note: Whenever we talk of a model 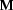 from now on, we mean a model of this vocabulary, and whenever we talk of formulae, we mean the formulae built from the symbols in that vocabulary.) We now give two further technical definitions which will enable us to state the satisfaction definition in a concise manner.
from now on, we mean a model of this vocabulary, and whenever we talk of formulae, we mean the formulae built from the symbols in that vocabulary.) We now give two further technical definitions which will enable us to state the satisfaction definition in a concise manner.
Interpretations.
First, let 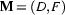 be a model, let
be a model, let  be an assignment of values to variables in
be an assignment of values to variables in 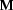 , and let
, and let  be a term. The interpretation of
be a term. The interpretation of  with respect to
with respect to 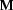 and
and  is
is 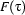 if
if  is a constant, and
is a constant, and 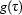 if
if  is a variable. We denote the interpretation of
is a variable. We denote the interpretation of  by
by 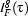 .
.
Variant Assignments.
Another concept we need is that of a variant of an assignment of values to variables. So, let  be an assignment of values to variables in some model, and let
be an assignment of values to variables in some model, and let  be a variable. If
be a variable. If 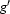 is an assignment of values to variables in the same model, and for all variables
is an assignment of values to variables in the same model, and for all variables  such that
such that 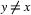 ,
, 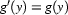 then we say that
then we say that 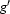 is an x-variant of
is an x-variant of  . Variant assignments are the technical tool that allows us to try out new values for a given variable (say
. Variant assignments are the technical tool that allows us to try out new values for a given variable (say  ) while keeping the values assigned to all other variables the same.
) while keeping the values assigned to all other variables the same.