10.1.2 Extending our Calculus: The Universal Rule
Adding a treatment of quantification to the inference processes discussed so far.
In this section we extend our calculus to first-order logic with quantifiers. To do so, we have to add a treatment of quantification to the inference processes discussed so far. This means that we have to give rules for the quantifiers under both polarities.
New Rules: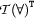 
, and 
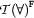
Remember we confined ourselves to a minimal set of propositional connectives (only 
and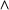 
), treating the others as defined. Likewise we shall confine ourselves here to giving rules for the universal quantifier 
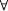and think of the existential 
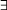as defined in terms of the equivalence 
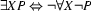. Due to this equivalence, the rule for the universal quantifier with negative polarity (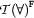) is in essence a rule for existential quantification. We will sometimes call it ``the existential rule'' (in contrast to 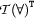, ``the universal rule''). We will later give derived rules that deal with the existential quantifier directly.
The Universal Rule
Let's first have a look at the universal rule. Whenever we have a generalized sentence, we know that we can put it concretely about every single individual we know of. When we have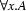 
, then we must also have 
for any individual that we ever come to know of. Let's think of ``we have for an individual named 
'' as ``we know , with all occurences of the variable 
in replaced by the constant ''. Then, the following rule is a straightforward formalization of our considerations:
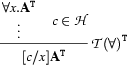
Multiple Applications
To understand this rule, we have to introduce the concept of a Herbrand base (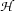
) of a tableaux branch. The Herbrand base of a tableaux branch is the set of constant symbols occuring on that branch. The rule 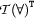allows to instantiate the scope of the quantifier with any constant symbol of the Herbrand base (the notation 
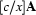means that we substitute for all occurences of in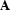 
). It may be necessary to apply the 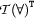rule to one and the same formula with multiple or even all constants on a branch. To achieve a complete calculus we thus have (in contrast to all other rules) to allow for multiple application of this rule to one formula.
Up to now, we have only made sure that the rule is justified if we read it from the antecedent to the succedent. But remember that it is crucial that the rules are also justified read in the other direction, i.e. the truth of the succedent guarantees the truth of the antecedent. But in fact, this is also the case here: when we have for any individual that we ever come to know of, then we must also have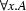 
. It can be shown that we can safely stick to cases where all individuals are named by some constant for tableaux-inference.
Let us now look at an example where one universal formula has to be instantiated twice to close a tableau. We will construct a tableaux proof for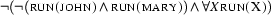 
. Intuitively, we would expect this to be a theorem. It states that it's impossible that John and Mary don't run, but still everyone runs. This is clearly a truism. And in fact with our new rule, we can have a tableaux proof of this formula as follows (we've coloured the premiss and results of the 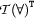-rule pink):
Using it
We achieve the closed tableaux by first instantiating the universal quantification with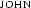 
(closing the left branch) and then with 
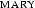(closing the right branch). Intuitively, to show that neither John nor Mary runs, we have to derive this fact once for each of them. One instantiation alone would not suffice.
?- Question!
As we will learn, the possibility to re-apply the 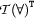-rule represents the main computational problem of first order inference. Can you already see why it is so problematic?