5.2.3 Summing up
Let us now sum up what we've done in the example with the help of a few more concise definitions. We've decomposed a formula in a tree that represents a set of case distinctions for satisfiability, or in other words, a set of candidate models. We started with an initial tableaux containing only one node with one signed formula.
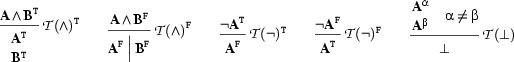
These inference rules act on tableaux. They have to be read as follows: If the formulae above the line appear in a tableaux branch, then the branch can be extended by the formulae or branches below the line. There are two rules for each primary connective - one for each sign. Additionally, there is a rule that adds the special symbol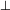 
to branches that contain (atomic) contradictions.
We have only given the rules for conjunction and negation. The other connectives can be defined as usual: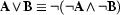 
, 
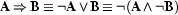
Open, Closed, Saturated
We call a tableaux branch closed iff it contains 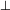, and open otherwise. We will call a tableaux closed, iff all of its branches are closed, and open otherwise. We use the above tableaux rules with the convention that no occurence of a formula is expanded more than once. We will call a branch (and also a complete tableaux) saturated if it is fully expanded, i.e. if no rule can be applied to it sticking to the convention just introduced.
Termination
This convention helps us ensure that the tableaux construction process always terminates (at least for propositional logic). Our inference rules always eliminate the primary logical connective from their antecedent (except for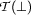 
). So, their succedents always have fewer logical connectives. As a consequence, the tableaux construction process terminates when all of the connectives are used up. In this case the formulae on all branches have been reduced to so-called literals and the tableaux is saturated. Alternatively, branches may be closed (by 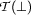) before they're saturated. Of course they need not be further expanded in this case either.
Tableaux Proof
We will call a closed tableaux with the signed formula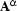 
at its root a tableaux refutation of 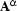, and we will call a tableaux refutation of 
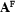a tableaux proof for 
.
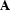If a branch is closed, this means that there is no model for the formulae on that branch taken together; and if a tableaux is closed altogether, this means that there is no model for the input formula at all. Constructing a tableaux proof for 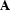means performing an exhaustive search for models that give 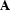the truth value 
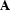. If all branches are closed, this search has failed and so cannot have the truth value . Thus 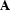must evaluate to 
in all models, which is just our definition of validity. So a tableaux proof for 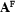can be constructed iff 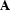is valid. To formally prove this fact (that is to establish correctness and completeness of the tableaux-method), one has to make the relation between branches and models more precise. The reader is referred to the literature to see how this can be done.