5.2.2 Tableaux for Theorem Proving (continued)

Disjunctive Expansion

We continue our tableaux construction by expanding the formula 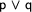. Under what conditions is this formula true? There are two possibilities: Either 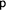is true or 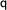is true. We express this in a tableaux by introducing a branching (we call this a disjunctive expansion):

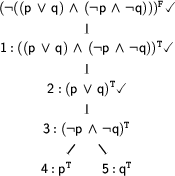
On each new branch, we pursue one of the possibilities to make the decomposed formula true. Now there is only one complex formula left to be expanded: 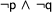. This expansion is like the second expansion again: The formula is true if both subformulae are true. So, we add these formulae conjunctively.

But to which branch should we add the new formulae? The answer is: to both. The expanded formula occurs on both branches and so both should get to see the result.

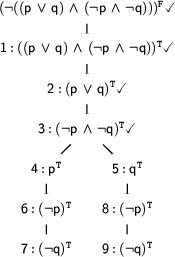
This time there are four expansions that we could apply next: We could expand node 6 or 7 on the left branch, or node 8 or 9 on the right one. We choose to expand nodes 6 and 9 next. The expansion of node 6 gives us 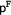on the left branch and the expansion of node 9 gives us 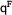on the right branch.

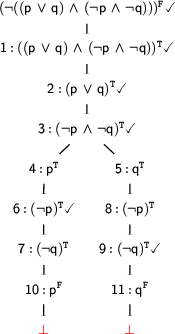
(Signed) Branch Closure

If you look at the tableaux, you will see that after these two expansions we have added a to both branches. We use to mark branches that contain a contradiction (i.e. two occurrences of the same atom with different signs). For example the left branch of our tableaux contains the contradiction 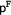and 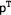. Such branches are called closed.

This is important because each branch with a contradiction represents a failed attempt to make the input formula false. So if all branches contain contradictions, there's no way to make the input false - exactly what we wanted to know. Since this is the case in our example, we know that our input formula is always true, i.e. valid. On the other hand, if one branch had still remained contradiction-free after expanding all of its complex formulas, that branch would show a way to make the input formula false. In other words, it would specify a model in which the input formula is false, that is a model for its negation.

Branches enumerate models

In general, each fully-expanded contradiction-free tableaux branch represents a model. A model for the negation of the input formula if, as in our example, the input formula is signed , and a model for the input formula itself otherwise. (In the first case, the must be ``translated'' into normal negation ). Moreover, all contradiction-free branches together specify all models of the (negated) input fomula.

Given this, let's state in terms of models what we've shown: Both branches of our example tableaux contain a contradiction. Therefore we know that there is no model for the formula 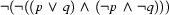(where we have translated the negative sign into negation). So 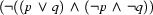is true in all models, that is valid.