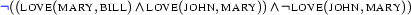5.2.4 Using Tableaux to test Truth Conditions and Entailments

Let us look at some further examples. To make things more interesting, we will use our proof method with a fragment of first-order predicate logic that allows us to express simple natural language sentences without introducing the whole complications of (undecidable!) first-order inference. Our fragment uses formulae of first-order logic, but without variables and quantifiers. This means that it is equivalent to propositional logic in expressivity: atomic formulae take the role of propositional variables.

We will first prove the implication ``If Mary loves Bill and John loves Mary then John loves Mary.''. We do this by exhibiting a tableaux proof of the formula

which is equivalent to

if we eliminate the defined connective . By exhaustively applying the inference rules above, we arrive at the following tableaux.

This tableaux has only one branch, which is closed. So the whole tableaux is closed and constitutes a tableaux proof for our implication.

?- Question!

Annotate each of the nodes of the above tableaux with the rule that has been used to add it.

As a second example let us now look at a variant problem:

1. ``Mary loves Bill or John loves Mary'' 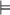``John loves Mary''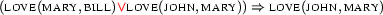

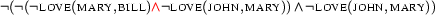
2. 

3. 

To prove the entailment (1) we represent it as an implication (2). Recall that the deduction theorem allows us to do so. We then eliminate the implication, arriving at (3).

Intuitively, (1) does not hold, because in the situation where the antecedent of the implication is true (i.e. Mary loves Bill), John need not love Mary. If we try to prove the entailment using our tableaux method, we get:

The tableaux we've just constructed is saturated (so we cannot expand it any further) and not closed. In fact, as we've already convinced ourselves above, our initial entailment conjecture doesn't hold, and so there is no tableaux proof for it.

A Model on an Open Branch

But we know more. The open and saturated branch represents a way of giving the input formula the truth value indicated by the sign, that is, a model for its negation. Let's see how. The literals on the open branch of the above tableaux (marked green) taken together characterize the situation in which the conjectured entailment fails to hold (namely the situation where Mary loves Bill but John does not love Mary). These are the ``minimal requirements'' on a model for the negated input formula.