11.4.4 A second example (universal quantification)

A second example for DRS threading.

How does DRS-threading extend to sentences containing determiners such as ``every''. Let's give a threading analysis of \nl{Every man runs}.

The semantic information associated with the the determiner ``every'' is a complex structure: an implicational condition consisting of two DRSs. This is shown in the analysis for the noun phrase \nl{every man} (we assume that the ingoing DRS is empty):

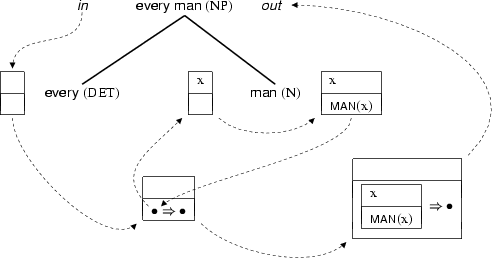
The outgoing DRS for ``every'' is the ingoing one to which an implicational condition (that is, an arrow linking two sub-DRSs) has been added. We don't yet know what the contents of these sub-DRSs are, so we represent each of them with a black hole . Actually, we do know a little more: this implication is a universal quantification, hence the antecedent black hole must contain a discourse referent x; this is indicated by the third threading arrow. How is the condition set of the antecedent to be filled? By the contribution of the noun (``man'' in this example), as the fourth threading arrow indicates. In short, once we've threaded every node in the noun phrase through the initial DRS, we will have successfully filled in the antecedent black hole and now are ready to pass on the resulting incomplete DRS (incomplete because the consequent is still just a black hole) to the rest of the sentence for further threading. But before going any further, let's express this noun phrase analysis in Prolog. First, the semantic marcro determiners that introduce universal quantification:

detSem(uni,[drs:Drs,ana:[in:A,out:A]]):-
   Drs = [in:[drs(D,C)|S],
          out:[drs(D,[Y>Z|C])|S],
          restr:[in:[drs([],[]),drs(D,C)|S],out:[Y|T]],
          scope:[in:[drs([],[]),Y|T],out:[Z|_]]].

Note that we have added two DRS-threading pairs: restr, which builds the DRS for the restriction (the first , represented by the Prolog variable Y), and scope which builds the DRS for the nuclear scope (the second , represented by Z). The outgoing DRS equals the ingoing DRS plus a new implicational condition.

Now for the combine rule that combines a determiner and a noun to form a noun phrase:

combine(np1:NP,[det:Det,n2:N]):-
   NP = [arg:Arg,drs:Drs,ana:[in:A1,out:A3]],
   Det = [drs:Drs,ana:[in:A1,out:A2]],
   N = [arg:Arg,drs:Restr,ana:[in:A2,out:A3]],
   Drs = [in:_,out:_,restr:Restr,scope:_].

Here Drs stands for the DRS-pair corresponding to the the overall DRS, and Restr for the DRS-pair that fills the first hole (the restriction of the quantifier). So, we now have an analysis for ``Every man'', but this contains a black hole marking the missing nuclear scope information. How do we fill it? The verb phrase takes care of this, as the following analysis shows:

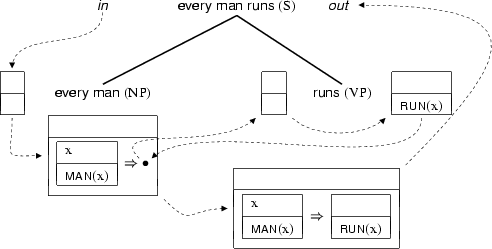
That is, we start threading the VP with an empty DRS and substitute the result for the black hole in the consequent of the implicational condition introduced by ``every''.

This completes our threading analysis of ``Every man runs'', and all important the ingredients of DRS-threading have now been discussed.