11.4.3 A First Example

A first example of threading.

Let's look at a first example. How would threading work for intransitive verbs?

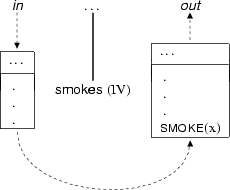
Note that the domain of the outgoing DRS is equal to the domain of the ingoing DRS, and that the condition set of the outgoing DRS consists of the conditions of the ingoing DRS ``plus'' the basic condition introduced by the verb. It is clear that the node has simply made the expected semantic contribution as it was threaded through the DRS.

In the threading approach every node is associated with an ``ingoing'' DRS, and an ``outgoing'' DRS, and the difference between the ingoing and outgoing DRS is exactly the information that is contributed by the syntactic category. The good news is that thinking in terms of ingoing and outgoing DRSs can be coded in Prolog in a straightforward and declarative way. To capture the effect of the previous diagram, the semantic macro for an intransitive verb must be:

ivSem(Sym,[arg:Arg,drs:Drs,ana:[in:A,out:A]]):-
   compose(Cond,Sym,[X]),
   Arg = [subj:X,obj:_],
   Drs = [in:[drs(D,C)|S],
          out:[drs(D,[Cond|C])|S]].

There are three important points to be made at this point. First, note that a semantic representations is not a single unit, but a recursive feature structure. On the top level we have arg, for argument information, and drs, containing the in- and outgoing DRS, labelled by in and out respectively. The third top-level feature ana collects constraints on anaphoric bindings as we will see later.

Second, note that we are keeping track of the discourse referent X used as the argument of the verb. Thirdly, note that we are not threading a single DRS around nodes (as shown in the diagram), but a list of DRSs. The reason for this extra bookkeeping will become clearer shortly when we will be discussing more complex examples.

Let's now give a threading analysis of the sentence ``Mia dances''. First, we need to add a lexical entry for the proper name ``Mia''. Proper names introduce both a discourse referent and a condition. The following diagram shows what happens when a node labelled by ``Mia'' is threaded through a DRS:

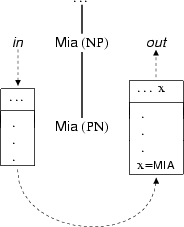
The following semantic macro turns this picture into a set of constraints:

pnSem(Sym,[arg:[index:X],drs:Drs,ana:[in:A,out:A]]):-
   Drs = [in:[drs(D,C)|S],
          out:Out,
          restr:_,
          scope:[in:[drs([X|D],[X=Sym|C])|S],
                 out:Out]].

As this macro shows, we introduced a number of new features here. Besides in and out, we also have restr and scope. These will play a role when we introduce quantified noun phrases (as we will explain in a moment), and the reason that we use them here for proper names is to keep the semantic representations in our grammar uniform and consistent.

That's the situation in the lexicon. So let's now see what happens as the DRS representing the previous discourse slides its way around the parse tree for ``Mia dances'' (in the following diagram we assume that the initial DRS is empty):

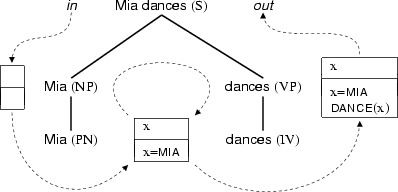
The semantic rule that takes care of the threading of the NP and VP nodes is coded as follows:

combine(s1:S,[np2:NP,vp2:VP]):-
   S = [drs:Sem,ana:[in:A1,out:A3]],
   NP = [arg:[index:I],drs:Sem,ana:[in:A1,out:A2]],
   VP = [arg:[subj:I,obj:_],drs:Drs,ana:[in:A2,out:A3]],
   Sem = [in:_,out:_,restr:_,scope:Drs].

These constraints ensure that the information is packed into the DRS correctly. Note that the extra arguments percolated upwards by the noun phrase and verb phrase are unified; this ensures the correct bindings of the discourse referent with its conditions.

In Section 11.4.7 when we discuss pronon resolution, we will see how constraints on anaphoric bindings are collected in the ana feature. What you can see here already is that these constraints are passed through such that all constraints end up on the sentence level.