3.4.9 Summing Up

Summing up the virtues of -calculus for semantic construction.

Let's sum up what we have achieved. Our decision to move to the disciplined approach of the 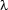-calculus was sensible. For a start, we don't need to spend any time thinking about how to combine two semantic representations - functional application and 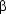-conversion give us a general mechanism for doing so. Moreover, much of the real work is now being done at the lexical level; indeed, even the bothersome problem of finding a decent way of handling NP representations uniformly now has a simple lexical solution.

What's next?

For the remainder of this lecture, the following version of the three tasks listed earlier will be put into practise:

Task 1

Specify a DCG for the fragment of natural language of interest.

Task 2

Specify semantic representations for the lexical items with the help of the 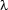-calculus.

Task 3

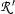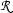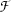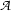Specify the translation of a syntactic item whose parts are and with the help of functional application. That is, specify which of the subparts is to be thought of as functor (here it's 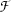), which as argument (here it's 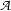) and then defin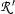e to be 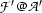, where 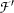is the translation of 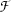and 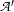is the translation of 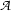. Finally, apply 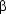-conversion as a post-processing step.