10.2.2 Universal Rule: Which Individuals to use?

Implementation of the universal rule.

As we have seen, our implementation of the 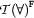-rule does not differ essentially from the propositional rules: We decompose an input formula and continue the tableaux building process with a less complex output formula. This means, that we practically throw away the input formula once we have decomposed it.

Quantifier must see all individuals

Can we proceed like this in the 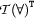case as well? We can't. Recall that (in contrast to all other rules) we have to be able to apply the 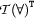once with every individual. Suppose that a branch stands for the model 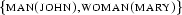at some time. If we now analyse a quantified formula like 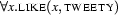, it's not enough to apply 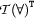only once, say with 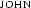. We have to be able to instantiate its scope with both individuals and get 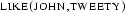and 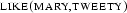. And moreover if later a new individual, say 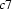is introduced, we have to be able to conclude 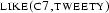. So simply throwing away the quantified formula will never be possible. We have to keep it somewhere in case we have to re-apply 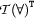later.

Store the quantifier

How can we do this in our implemetation? Our solution is quite simple: Whenever we analyse a formula of the form true(forall(X,Scope)), we not only instantiate Scope with one of the currently known individuals. We additionally put the quantified formula on a list so that we can re-use it later on. This is why our tabl/6 predicate now has the additional arguments QuantsIn and QuantsOut. They serve to store the quantified formulae thus collected. We will refer to the list represented by this pair of arguments together as quants in the next sections.

Passing through

Thus each part of a tableaux may add one or more quantifiers to our quants-list (much like it possibly extends the model (branch), (see Section 8.1.1)). If you look at the conjunctive clause with the new arguments, you can see that the second call of tabl/6 gets the resulting quantifier list (QuantsOut1) of the first call of tabl/6 as input:

tabl(true(A & B),InBranch,OutBranch,QuantsIn,QuantsOut,Qdepth) :-
        !,tabl(true(A),InBranch,K,QuantsIn,QuantsOut1,Qdepth),  
        tabl(true(B),K,L,QuantsOut1,QuantsOut,Qdepth),
         list_to_set(L,OutBranch).

The second call can thus see the universally quantified formulae found in the first call (and possibly re-apply 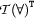to them).