10.2.1 The Existential Rule

Implementation of the existential rule.

Let us recapitulate our two new rules. Let us first look at the 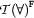-rule. In Prolog, we write negative universal formulas as false(forall(x,Scope)). When we encounter an existential formula, we first introduce a new constant and then generate a new formula by substituting the new constant for the quantified variable x in Scope. E.g. false(forall(x,walk(x))) will license false(walk(c7)) where c7 is a new constant.

foTabl.pl: View Download

If we ignore the additional arguments of tabl/6 for a moment, our implemented 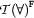-rule (to be found in foTabl.pl) should be relatively easy to understand:

tabl(false(forall(X,Scope)),InBranch,OutBranch,QuantsIn,QuantsOut,Qdepth) :-
        !,newconst(NewConst),
        subst([X:NewConst],Scope,NewFormula),
        tabl(false(NewFormula),InBranch,OutBranch,QuantsIn,QuantsOut,Qdepth).

signature.pl: View Download substitute.pl: View Download

The call to newconst/1 (from signature.pl) creates a new constant of the form c1,c2... (using a counter). The predicate subst/3 (from substitute.pl) in the case at hand does the same as the substitute/3 we used in earlier chapters. It takes a substitution, e.g. [x:c7,y:c5] and a formula as input and returns the result of applying the substitution to the formula.