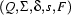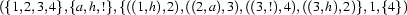3.1.4 Regular Expressions and FSAs

Regular expressions and FSAs are equivalent.

Now that we know precisely what regular expressions are, let us look systematically at their relation to FSAs. As we've already mentioned, both formalisms are equivalent. They both characterize the same set of languages known as the regular language s. We shall now prove one direction of this equivalence: If is a regular expression, then there exists a FSA that accepts the language characterized by . Proving this basically means stating more formally what we illustrated by examples in Section 3.1.2. To do so let us first introduce a canonical notation for FSAs. We write a FSA as a quintuple:

In such a quintuple

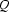
is the set of states of the automaton.

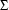
is the alphabet underlying the language characterized by the automaton.

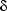
specifies what transitions can be made in the automaton

is the start state of the automaton.

F

is the set of final states of the automaton.

How does 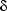specify what transitions can be made? It states for each state-symbol-pair in the automaton, where the transition from the respective state over the symbol leads. So 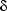is a relation over 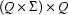. We can also require that 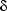be a function, making the automaton deterministic.

Let's compare our canonical way of specifying a FSA to our Prolog notation from Section 1.4: There, we specified possible transitions (i.e. 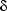) by giving trans/4-terms. The initial state () was given as a start/2-term, and the final states () in the form of final/2-terms. The set of states 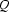as well as the alphabet 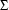were left implicit. Here's how we formally specify the laughing machine from Section 1.3: