3.1.3 Definition of Regular Expressions

Definition of regular expressions.

But before we have a closer look at this systematic relation between regular expressions and automata, let's give a more formal statement of what a regular expression is and what language it denotes.

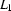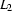First here's some notation to (independently, in terms of sets) describe languages. Let , and be languages over a (finite) alphabet 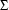(i.e., subsets of the set of all strings that can be formed from 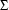). Then

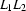
denotes the concatenation of these two languages, that is the language that contains all strings formed by concatenating a string from 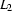to a string from 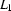(picking a string from 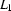and following it by one from ).

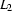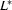
denotes the Kleene closure of . It contains all strings obtained by concatenating any number of strings from . In particular it contains the empty string as the result of concatenating zero strings from .

Definition

Now we're ready to turn to regular expression s themselves. Again given an alphabet :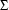

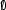and

are regular expressions denoting the empty language, 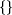, and the language containing only the empty string, 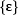. Note that these two languages are different.

for each 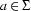is a regular expression and denotes 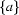, the language consisting of the single symbol .

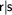, and

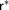
are regular expressions, provided r and s are. If denotes the language and denotes the language , then denotes their concatenation 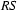, 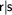denotes their union 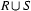, and 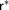denotes the Kleene closure of , .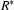