11.2.3 Syntax of DRSs and DRS-Conditions

The formal, recursive definition of DRSs and DRS-Conditions.

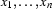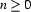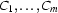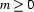1. If are discourse referents () and () are DRS-conditions then the following is a DRS:

   

2. If is a relation symbol of arity ( 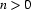), and 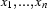are some discourse referents, then 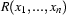is a DRS-Condition;

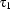3. If and 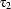are first-order terms, then 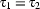is a DRS-Condition;

4. If and 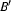are DRSs, then 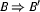and are DRS-Conditions;

5. If is a DRS, then is a DRS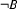-Condition;

6. Nothing is a DRS or DRS-Condition unless it can be shown to be so using clauses 1-5.

Here, first-order terms (clause 3) denote either discourse referents or constants. We sometimes refer to DRS-Conditions of the form licensed by clauses 2-3 as ``basic'' conditions, while those licensed by clauses 3-5 are called complex conditions. Note that, in a way, DRSs bear a lot of similarities with the first-order logic formula syntax. As in first-order logic, we have the boolean connectors (, , 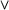) to create nested boxes and express implication, disjunction, and negation. But unlike first-order logic, we don't have explicit conjunction, and we don't have explicit quantifiers. With a formal definition of the syntax of DRSs at our disposal, we are now in a good position to define subordination (a relation between DRSs), which then opens the way to define accessibility.