Consequences for Theorem Proving

As we've already said, the presence of quantifiers gives a huge boost in expressivity. We were happy to benefit from this fact. But with the loss of the finite model property we can now see the dark side of it. The consequences also extend to the use of tableaux for theorem proving. We can already easily see that if quantifier alternations like the -constellation in our example can keep us busy forever, we must be careful that they do not keep us from finding contradictions that would close our tableaux.

As we've already said, the presence of quantifiers gives a huge boost in expressivity. We were happy to benefit from this fact. But with the loss of the finite model property we can now see the dark side of it. The consequences also extend to the use of tableaux for theorem proving. We can already easily see that if quantifier alternations like the 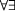-constellation in our example can keep us busy forever, we must be careful that they do not keep us from finding contradictions that would close our tableaux.

Loosing Decidability

In short, all our problems relate to the fact that first-order satisfiability is no longer decidable. So we have bought the added representational power with a loss of computational tractability. But we know what the problems are, and with this in mind, we can continue our theoretical considerations. Still for the implementation of our calculus, we really have lost something essential. Recall that decidability of PLNQ, termination of the tableaux calculus for it, and termination of our implementation were all closely connected. Now that we've lost decidability, we cannot have a complete and correct calculus that terminates in general. Of course we have to keep this in our mind when we extend our implementation - we will see that termination comes only at the cost of completeness. We will always have to invest a good deal of thought and work to arrive at an implementation that terminates but still gives useful results in many interesting cases. This is what we will do in the next section.

?- Question!

Things could be worse: At least first order satisfiability is semi-decidable . This means that whenver a formula is not satifiable, we can find this out by a finite computation - a matter of great importance to tableaux based theorem proving. Why is it so important?