9.1.4 Tableaux generate Herbrand Models
Tableaux generate Herbrand Models.
The literals on an open saturated tableaux branch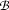 
are a Herbrand model 
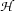, as we have convinced ourselves above. Is this all we wanted to show? No! We still have to argue that 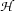is also a model for the input formula of the tableaux.
From the Literals to the Input Formula
The argument goes as follows: The tableaux inference rules are made up in a way that whenever a model satisfies the succedent, it also satisfies the antecedent (which is immediate from the semantics of the principal connectives). So, if 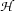is a model of the literals of 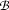, then it is also a model of the complex formulae on 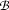which were decomposed into these literals during the tableaux construction. Transitively, this argument shows that 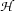is a model of all formulae on .
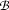In particular, 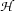is a model for the input formula of the tableaux, which is on 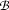by construction. So the tableaux procedure is also a procedure that generates explicit (Herbrand) models for the input formula of the tableaux. Every branch of the tableaux corresponds to a (possibly) different Herbrand model.
Finite Model Property
As we have already seen, tableaux saturation always terminates for PLNQ. As a consequence, every Herbrand model we generate is represented by a finite set of literals. But if we look at the construction of such a Herbrand model, we see that it is also finite in a different sense: its domain is finite. Because all of the Herbrand models generated for PLNQ formulae by our tableaux procedure are finite, and our tableaux procedure is complete, we can be sure that satisfiable PLNQ formulae always have a finite model. This property of a logic is called the finite model property .
Decidability
Another consequence of termination of tableaux saturation together with the fact that tableaux enumerate all possible models is that model generation is a decision procedure for satisfiability in PLNQ, i.e. an algorithm that will determine the satisfiability of any PLNQ formula in a finite time.