7.2.3 Analytical Tableaux: A more formal Account
Formal definition of tableaux.
Let us now sum up what we've done in the example with the help of a few more concise definitions.
Signed Formulae
The calculus of analytical tableaux analyzes a formula in a tree that represents a set of case distinctions for satisfiability. The calculus we will use acts on signed formulae, i.e. formulae decorated with an intended truth value. A formula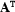 
signifies that the calculus tries to satisfy the formula 
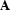, whereas 
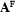shows that the calculus tries to refute it.
Initial Tableaux
The tableaux proving process starts with an initial tableaux that contains only one node with one signed formula.
Tableaux Inference Rules
The tableaux is then generated by applying the following inference rules
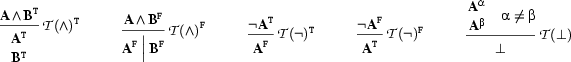
For the moment we have only given the rules for conjunction and disjunctions, since the other connectives can be defined in terms of these (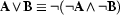
, 
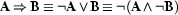). We will extend the calculus later.
These inference rules act on tableaux. They have to be read as follows: If the formulae above the line appear in a tableaux branch, then the branch can be extended by the formulae or branches below the line. There are two rules for each primary connective - one for each sign. Additionally, there is a branch closing rule that adds the special symbol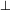 
(for "closed") to branches that contain contradictory literals.
Open, Closed, Saturated
We will call a branch in a tableaux closed iff it contains 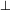, and open otherwise. We will call a tableaux closed, iff all of its branches are closed, and open otherwise. We use the above tableaux rules with the convention that no occurence of a formula is expanded more than once. We will call a branch (and also a complete tableaux) saturated if no rule can be applied to it, sticking to this convention.
Termination
The convention helps us ensure that the tableaux construction process always terminates (at least for the quasi propositional logic PLNQ that we will introduce in a minute). The inference rules just given always eliminate the primary logical connective from their antecedent (except for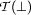 
). So, their succedents always have fewer logical connectives. As a consequence, the tableaux construction process terminates when all of the connectives are used up and the formulae on all branches have been reduced to literals (in other words, when the tableaux is saturated). Alternatively, branches may be closed (by 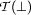) before they're saturated. Of course they need not be further expanded in this case either.
A stronger version of our convention allows rule application only if it adds new material (i.e. if the result does not already occur on the branch). In Section 10.2.6, we will need this stronger control mechanism when we deal with first-order tableaux expansion.
Tableaux Proof
As we have discussed already, if a branch is closed, this means that there is no model for the formulae on that branch taken together; and if a tableaux is closed altogether, this means that there is no model for the input formula at all. Constructing a tableaux for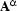 
means building up an exhaustive case analysis of what is necessary to give 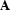the truth value 
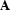. If all branches are closed, this means that all cases in this analysis lead to contradictions, and so cannot have the truth value .
We will call a closed tableaux with the signed formula 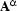at its root a tableaux refutation of 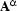, and we will call a tableaux refutation of 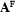a tableaux proof for 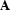. It refutes the possibility of finding a model where 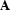evaluates to 
. Thus 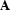must evaluate to 
in all models, which is just our definition of validity.
Positive vs. Negative Calculi
So the tableaux procedure gives us a notion of proof and can thus be used as a calculus for proving theorems. But as we have seen it does not prove a theorem directly by deriving it from a set of axioms (like the calculus in Section 7.1.3 does). Instead it proves it by refuting its negation. A proof that works indirectly like this is also called a refutation proof . A calculus that leads to a refutation proof is called negative or test calculus . Generally negative calculi have computational advantages over positive ones, since they have a built-in sense of direction.