Course Schedule

One question ahead

One question that we have to answer in the first place

But there's one more question, which we have to answer in the first place: Meaning as such is a very abstract concept. It's not at all easy to imagine what it means to ``work with meanings'' directly. So what are we going to do? To study meaning, and especially to deal with it on a computer, we need a handle on it, something more concrete: We shall work with meaning representations - strings of a formal language that has technical advantages over natural language. In this course, we will represent meanings using formulas of first order logic. First order logic gives us (at least) two things: First, a formal language with desirable properties such as having a simple, well defined (and unambigous) syntax. This makes it fit for use with the programs we're going to implement. Second, there is the truth-functional interpretation telling us unambigously under which conditions formulae hold and what the symbols they're made of mean. In other words, we have a formally precise conception of how our first order meaning representations relate to certain situations in the world. So, via meaning representations we come a step closer to understanding how sentences manage to convey something about how the world is.

First Order Logic

Contents of the first two lectures of the course: FOL and its representation in Prolog.

First order logic and Prolog

The first two lectures of this course pave the way for the rest. They're directly concerned with first order logic, the meaning represenation language that everything we're going to do in this course is based upon. Chapter 1 contains the basic concepts of first order logic, giving us the background we need in order to understand how our representation language works. We will explain central terms of first order logic, such as first order formula, model, satisfaction and truth in a model. This lecture serves as a repetition and as a reference for later chapters. In Chapter 2 we then turn to the computational side of our enterprise. We show how to represent first order formulae and models in Prolog. Furthermore, we will see how to make sense in implementational terms of the definitions given in the previous lecture, We will look at the example of the definition of truth in a model and implement a small model checker.

In the next three lectures (which form the first main part of this course) we will mainly use first order logic in virtue of its nice properties as a formal language. We will not talk about truth or models for formulae. Still of course, these notions remain in the background as the main reason why we say for instance that the meaning of ``Every man walks'' is captured by the first order formula 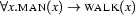. They will become the focus of our interest again (although from a new perspective) in the second main part of the course, which deals with inference. So now for the two main parts.

Semantic Construction

The first main part of the course (consisting of lectures 3-6) is concerned with the task of semantic construction.

The first main part of the course (consisting of lectures 3-6) is concerned with the task of semantic construction. Because we use first order logic as our meaning representation language, our question from above now turns into: ``Given a sentence, how do we get to the first order formula that represents its meaning?''.

-Calculus

Chapter 3 shows that this is not a trivial question. Using a first, quite naive approach to the matter we will soon encounter a lot of problems. We solve these problems by introducing -calculus. This calculus has been a standard tool for semantic construction ever since the pioneering work of Richard Montague in the 1960s. It allows us to compose complex formulae in an elegant manner: Making use of 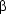-reduction, the key technique introduced with -calculus, we arrive at formulae of first order logic for natural language sentences by a stepwise simplification of other expressions that correspond to the structure of those sentences more directly.

As an application, we present an implementation of semantic construction in the spirit of Montague semantics. This allows us to automatically construct the first order representations for natural language input sentences such as ``A therapist loves a siamese cat''. You can test this implementation here. So by the end of this lecture, we will have our first program that masters the task of semantic construction for a small fragment of English. But there's still a lot to be done.

Implementation

Starting off from the Prolog program we've just developed, we focus on implementational considerations in the next lecture (Chapter 4): We take a second look at our program, this time from the perspective of software engineering. We redesign it from a single-purpose implementation into a more general and modular framework for semantic construction. This framework will easily extend and adapt to cover new sorts of semantic phenomena that we may encounter.

Scope ambiguities and Underspecification

Then, in Chapter 5, we return to the linguistic side and take a look at one such new class of phenomena: scope ambiguities. In the case of a scope ambiguity, multiple meanings are associated with one and the same sentence in a systematic way. This may happen e.g. because a sentence contains several quantified noun phrases (the infamous ``Every man loves a woman.'' is one such sentence).

The study of scope ambiguities has been a central issue in natural language semantics for a long time. We will first explain briefly why such ambiguities occur and then give a historical overview of how people have tried to deal with them. We explain why the early extensions of Montague semantics could not treat the central phenomena satisfactorily. Then we discuss the use of underspecified representations. Underspecified representations allow us to speak about the parts formulae (representing for instance ambiguous sentences) are made of, but we don't have to commit to one arrangement of these parts (i.e. one reading). This turns out to be the key to solving a whole bunch of problems scope ambiguities pose for semantic construction.

Finally, we turn to CLLS, a calculus for semantics construction based on underspecification. In Chapter 6 we implement this calculus and integrate it into our semantics construction framework. The resulting system allows us for example to get the five readings for the following sentence: ``Every owner of a siamese cat loves a therapist.''. You can run the program here. When we develop this implementation we shall greatly benefit of the work we put into re-designing our semantic construction program to a general framework in the previous lecture: We just have to give Prolog code for the interesting changes, while being able to re-use all of the periphery that we already have at hand.

Inference

In this part of the course (lectures 7-10) we approach the following question: Given that we have the meaning of a sentence, what can we do with it?

Up to this point in our course, we've mostly been concerned with the business of building a logical formula for a given natural language sentence that adequately describe its meaning (or - for that matter - several formulae for several meanings). Now, we are going one step further, approaching the second question we posed ourselves above: Given that we have the meaning of a sentence, what can we do with it?

The key idea that we will pursue when answering this question is that - intuitively speaking - doing something with the meaning of a sentence means finding out what follows. For example, when we know that Mutz is a siamese cat and we hear: ``John doesn't have any pet.'', we do something with the meaning of this sentence when we come to the conclusion that John isn't Mutzi's owner.

On the level of meaning representations, ``finding out what follows'' from a sentence means drawing inferences from the first order formula that corresponds to that sentence. Tasks of finding out what follows (that is, inference tasks) play an important role at many different stages in the process of understanding a sentence. In the example above we inferred from the formulae for a few sentences (often, we will also make use of additional world knowledge). This kind of inference may e.g. be neccessary to find out what the speaker intended us to do when he uttered the sentence, or it may help us to exploit the information the speaker conveys for our purposes. It extends to the interface between semantics and pragmatics (and sometimes beyond it). But inference may be of use in semantic processing already at much earlier stages. We can e.g. use inference mechanisms to find out what would follow from one reading of a sentence (as opposed to another one) when we have to decide whether to discard or prefer the reading, and base our decision on our findings..

Inference in Computational Semantics

For us as computational semanticists these are a lot of good reasons why we should try to get a grip on drawing inferences computationally. In Chapter 7 we take a closer look at techniques for this purpose. We introduce the notion of a proof as well as mechanisms to work with this notion. These mechanisms (called calculi) capture semantic concepts (like that of a valid argument, which we learned about in the first lecture) via methods for manipulating formulae (i.e. syntactic objects). They are therefore well suited for use in computational semantics - after all manipulating formulae is something that can be done by a computer.

The calculus we discuss in detail is that of (semantic) tableaux. In this lecture, we shall look at tableaux for propositional logic. One advantage of tableaux is that we can also use them to generate models for a given formula. As we shall see this offers a new perspective on a variety of natural language phenomena. Another advantage is that this calculus is good for direct implementation in Prolog. Something we shall prove in practice by giving such an implementation.

First Order Inference

In Chapter 10 we generalize to first order logic what we learned about propositional inference in the previous lecture. We extend our tableaux calculus, and change the implementation accordingly. While the calculus extends readily, extending the implemenation is not a trivial task at all. We will discuss why this is so, and then take the trouble of integrating what non-trivial additions and changes we need into our implementation.

Discourse Representation Theory

The last chapter.

Up until now our only concern was the meaning of single sentences. In this chapter, we look at discourse, i.e. sequences of sentences. Interesting challenges arise that go beyond the tools and techniques for computational semantics we have developed so far. One of these challenges is interpreting pronouns - words like he, she and it which indirectly refer to objects. In this chapter we will introduce Discourse Representation Theory (DRT) and show how one can build semantic representations of texts and develop algorithms for resolving pronouns to their textual antecedents.

And finally...

The End-term projects.

The proof of the pudding

And finally, the proof of the pudding is the eating: We've implemented a number of programs - a model checker, a semantics construction engine, an inference system. What can they do if they work together? Chapter 12 asks you to explore this. It contains a collection of exercises that are meant to be starting points for your end-term projects. Have fun!