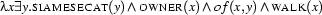12 The Proof of the Pudding is in the Eating

In the end of the course, you can review what you have learned by plugging together some of the modules developed earlier. What you will have to do is program some driver and auxiliary predicates. The code will not be more than one or two pages. Since this is the assignment formally documenting your work performed in this course, please add a doumentation of about two pages. Besides the description of your code, it should contain the input formulae, natural language sentences, etc. you used to test your programs.

12.1 End term projects

The following exercise together are a suggestion for an end-term project.

Exercise 12.1

Model Inspection
Design a natural language-interface (using -calculus) to our revised model checker. The idea is that you can inspect some predefined model like
example(4,[bird(tweety),siamesecat(mutzi),woman(mary),man(john),man(miles), love(miles,mary),owner(mary),of(mary,mutzi), love(miles,tweety),love(john,mary),walk(mary), therapist(mary),eat(mutzi,tweety)]).
by asking questions like
``Does John love Mary?''
``Which owner of a siamese cat walks?''
Hint: For the time being, a cursory treatment of questions is enough for our purposes here. It should lead to the following representations of the questions given above:
and
The expected answer to the first question is ``yes'' in the example. The answer to the second question should consist of all values of that make the scope of the abstraction true (in our case ``Mary'').

Exercise 12.2

Model Extension
Use our tableaux-based model generation procedure to extend models like the one presented in Exercise 12.1. An example run could look like this:
1 ?- extendModel(5,10). before: [bird(tweety), siamesecat(mutzi), woman(mary), man(john), man(miles) ,love(miles, mary), owner(mary), of(mary, mutzi), love(miles, tweety), love(john, mary), walk(mary), therapist(mary), eat(mutzi, tweety)] > john loves every siamese cat. after: [eat(mutzi, tweety), therapist(mary), walk(mary), love(john, mary), love(miles, tweety), of(mary, mutzi), owner(mary), love(miles, mary), man(miles), ~siamesecat(miles), man(john), woman(mary), ~siamesecat(mary), siamesecat(mutzi), love(john, mutzi), ~siamesecat(john), bird(tweety), ~siamesecat(tweety), ~siamesecat(*)]
This example also gives you an impression of what direct, uncontrolled model generation does. First of all, if a speaker utters ``John loves every siamese cat.'' in the situation described by our input model, one thing she probably wants to communicate is that ``John loves Mutzi''. But our system also has generated lots of other facts, such as ~siamesecat(john), that are not contradictory (up to now) although they probably weren't intended by the speaker. Moreover, the system has blindly chosen one of many possible extensions of the input model. Another possible extension would e.g. contain siamesecat(john), love(john,john) instead of ~siamesecat(john). Now what exactly makes the extension of mental models in human language understanding so much more focussed than what our implementation does? Do you have any ideas (speculate, you don't have to implement...)?

Exercise 12.3

Informativity Checking
Remember how we can use tableaux to check the informativity of a given formula with respect to some other formula(e) (see Section 7.2.5). Implement a little program that checks the informativity of a natural language sentence with respect to some world knowledge. For example suppose you have some world knowledge that tells you that ``Every human works'', that ``John is a man'' and that ``All men are human'':
wk(man(john) & forall(x,human(x)>work(x)) & forall(y,man(y)>human(y)) & forall(z,woman(z)>human(z))).
Now, your system should check the informativity of input sentences like this:
1 ?- checkInf. > john works. *** Doesn´t interest me... *** Yes 2 ?- checkInf. > john does not work. *** This is impossible! *** Yes 3 ?- checkInf. > tweety works. *** Maybe... *** Yes