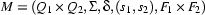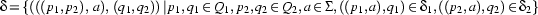3.2.2 Intersection, Complementation
The class of regular languages also has closure properties under intersection and complementation.
But the class of regular languages also has closure properties that are not obvious from the definition of regular expressions. We shall look at closure under intersection and complementation.
Intersection
If 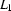 and
and  are regular languages, then so is
are regular languages, then so is 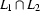 . We will now construct a FSA
. We will now construct a FSA 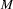 for
for 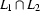 from two FSAs
from two FSAs 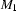 and
and 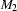 for
for 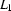 and
and 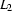 . The idea is to construct an automaton that simulates going through
. The idea is to construct an automaton that simulates going through 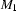 and
and 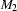 synchronously, step by step in parallel. Formally (we use indices 1 and 2 to refer to elements of
synchronously, step by step in parallel. Formally (we use indices 1 and 2 to refer to elements of 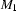 or
or 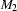 respectively, and assume that both automata share the same alphabet):
respectively, and assume that both automata share the same alphabet):
The states of the new automaton will are all pairs of states from 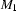 with states from
with states from 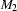 .
.
The transitions will be such that the paths through 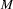 are the paths through
are the paths through 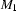 if we only look at the first element of each state-pair, and are the paths through
if we only look at the first element of each state-pair, and are the paths through 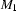 if we only look at second elements:
if we only look at second elements:
But our new automaton will accept a word only if the computation ends on a pair where both elements are final states in their ``original automata'' (the set of final states is specified as 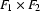 ). This means that we can reach a final state with a word in
). This means that we can reach a final state with a word in 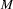 iff we could reach a final state with it in
iff we could reach a final state with it in 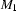 and in
and in 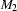 , hence iff the word is in
, hence iff the word is in 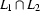 .
.
Complementation
If  is a regular language over an alphabet
is a regular language over an alphabet 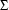 , then so is
, then so is 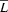 (i.e. the language consisting of all strings from
(i.e. the language consisting of all strings from 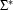 that are not in
that are not in  ). We will again show how to construct an automaton
). We will again show how to construct an automaton 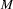 for
for 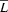 from an automaton
from an automaton 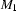 for
for  . Yet this time we have to make three additional assumptions:
. Yet this time we have to make three additional assumptions:
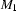 is
is  -free, i.e. contains no jump arcs.
-free, i.e. contains no jump arcs.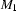 is complete, i.e. there is a transition from each state in
is complete, i.e. there is a transition from each state in 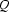 over each symbol in
over each symbol in 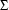 (note that none of the automata we've seen so far has had this property).
(note that none of the automata we've seen so far has had this property).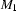 is deterministic.
is deterministic.
However, these assumptions are quite harmless. We can get rid of jump arcs by systematically substituting direct transitions over the symbols read before and after each jump. For example, look at the following very simple automaton with one jump arc:
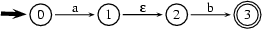
To get rid of the jump arc between states 1 and 2, we transform it into the following automaton:
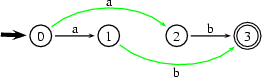
The two transitions we've added so to speak bypass the former jump arc.
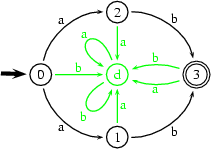
To complete an automaton we do as follows: We add one ``dead'' state (a new state that has no outgoing transitions to any other states), and let all the ``missing'' transitions point to it. For instance, here's a completed version of our  -free automaton from above:
-free automaton from above:
Finally, as we've already mentioned, non-determinism doesn't add anything substantial to FSAs, and every non-deterministic FSA can be transformed into a deterministic one. The algorithm fo this purpose is a bit more involved and we can present an easy example here. The basic idea is to build a new automaton that has as states all sets of states in the old one.
So for the construction of a complement-automaton, let's assume that 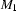 is a determinstistic
is a determinstistic  -free complete FSA for the language
-free complete FSA for the language  . Then we construct an FSA
. Then we construct an FSA 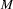 for
for 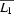 by copying
by copying 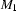 and making all and only its non-final states final states of
and making all and only its non-final states final states of 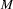 .
. 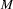 will reach a final state on a word (and thus accept it) if and only if that word would have taken
will reach a final state on a word (and thus accept it) if and only if that word would have taken 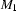 into a non-final state. Hence
into a non-final state. Hence 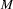 will accept all and only those words from
will accept all and only those words from 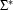 that are not accepted by
that are not accepted by 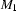 .
.
Notice that once we know that regular languages are closed under union and complementation, closure under intersection follows from the set theoretic fact that 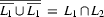 . An automaton for any intersection language can be contructed accordingly by nesting the construction methods for union and complementation. But because to prove closure under complementation, we had to make assumptions that we don't need for the direct construction method for intersection, we've chosen to present this direct method first.
. An automaton for any intersection language can be contructed accordingly by nesting the construction methods for union and complementation. But because to prove closure under complementation, we had to make assumptions that we don't need for the direct construction method for intersection, we've chosen to present this direct method first.