3.2.1 Concatenation, Kleene Closure and Union

The set of regular languages is closed under concatenation, union and Kleene closure.

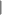It follows from the definition of the operators of concatenation, and that the set of regular languages is closed under concatenation, union and Kleene closure:

• If is a regular expression and is the regular language it denotes, then 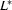is denoted by the regular expression 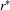and hence also regular.

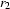• If and are regular expressions denoting 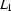and 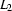respectively, then 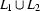is denoted by the regular expression 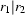and hence also regular.

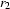• If and are regular expressions denoting 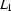and 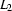respectively, then 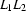is denoted by the regular expression 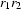and hence itself regular.

The rules for constructing FSAs based on these closure properties can be read off the respective parts of the inductive step of the proof in Section 3.1.5.