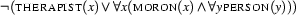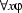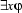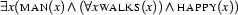1.2.4 Bound and Free Variables

Free and Bound Variables

Let's now turn to a rather important topic: the distinction between free variable s and bound variable s.

Have a look at the following formula:

The first occurrence of x is free, whereas the second and third occurrences of x are bound, namely by the first occurrence of the quantifier 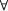. The first and second occurrences of the variable y are also bound, namely by the second occurrence of the quantifier .

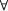Informally, the concept of a bound variable can be explained as follows: Recall that quantifications are generally of the form:

or

where may be any variable. Generally, all occurences of this variable within the quantification are bound. But we have to distinguish two cases. Look at the following formula to see why:

1. may occur within another, embedded, quantification 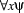or 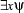, such as the in 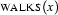in our example. Then we say that it is bound by the quantifier of this embedded quantification (and so on, if there's another embedded quantification over within ).

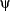2. Otherwise, we say that it is bound by the top-level quantifier (like all other occurences of in our example).

Here's a full formal simultaneous definition of free and bound:

1. Any occurrence of any variable is free in any atomic formula.

2. No occurrence of any variable is bound in any atomic formula.

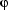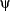3. If an occurrence of any variable is free in or in , then that same occurrence is free in 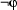, , 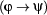, 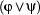and .

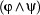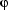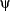4. If an occurrence of any variable is bound in or in , then that same occurrence is bound in 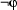, , 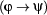, 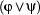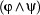. Moreover, that same occurrence is bound in 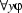and 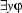as well, for any choice of variable y.

5. In any formula of the form 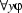or 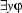(where y can be any variable at all in this case) the occurrence of y that immediately follows the initial quantifier symbol is bound.

6. If an occurrence of a variable x is free in 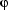, then that same occurrence is free in 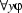and 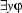, for any variable y distinct from x. On the other hand, all occurrences of x that are free in 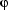, are bound in 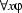and in .

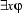If a formula contains no occurrences of free variables we call it a sentence .