3.5.1 Representations

Representation of -expressions in Prolog.

First, we have to decide how to represent -expressions in Prolog. Something as simple as the following will do:

lambda(x,F)

Be careful!

According to our convention, x is a Prolog constant representing the variable bound by the . F is (the Prolog representation of) either a first-order formula or a -expression. Note that in the system we are going to implement, you will often see Prolog variables in place of the x. In Section 3.5.3 you will see why.

Secondly, we have to decide how to represent concatenation. Let's simply transplant our @-notation to Prolog by defining @ as an infix operator:

:- op(950,yfx,@).         % application

That is, we shall introduce a new Prolog operator @ to explicitly mark where functional application is to take place: the notation F@A will mean ``apply function F to argument A''. We will build up our representations using these explicit markings, and then carry out 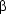-conversion when all the required information is to hand. So - as we discussed above - the @-operator will finally take over the role of the +-operator in our first attempt at semantic construction, and 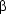-conversion will replace the post-processing formerly done by insertArgs/2.

?- Question!

We could as well perform 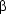-conversion steps interleaved with the construction of the application. For instance, we could always fully reduce the -expressions at the nodes of our syntactic trees before going on. Why? Look again at one of our previous examples and see how it works out if you 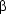-convert at different stages!