3.3.2 Putting Things in the Right Place I

Post-processing the output of our DCG for semantic construction: simple cases.

Obviously, in order to obtain true first order formulae, the output of our little DCG needs to be further processed. The problem is that our resulting expressions consist of parts of a first-order formula glued together, instead of one complete-first order formula with all of its parts in the right place. What do we have to do? Let us first have a look at a simple case: From parsing the sentence ``Mary walks.'' we get the term mary+walks(_). From this, we would like to obtain the first-order formula .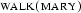

Postprocessing: Inserting the Arguments

In this example, we could do with simply inserting the item to the left of the + into the argument slot of the item to the right. The predicate insertArgs/2 does so:

insertArgs(N+V,V) :-
        compose(V,_,[N]).

Here is an example call: s(Sem,[mary,walks],[]), insertArgs(Sem,Inserted) .

What is going on here? Recall that the predicate compose/3 (see Section ``compose/3'') states that its first argument consists of a functor (given as first argument) and arguments (second argument, a list). In our example, the call to compose/3 states that the term walk(_) is to consist of a functor (which is unified with the anonymous _) and exactly one argument, which is unified with N. Now N is in turn instantiated to mary, and so of course the only solution is walk(mary).

Would this strategy of "left-to-right-insertion" work in general? It wouldn't. Recall that we obtained the term john+(love(_,_)+mary) for the sentence ``John loves Mary.''. In this case, the lexical representation for the verb has two argument slots. Moreover, it occurs to the left of one + and to the right of another at the same time. Our predicate insertArgs/2 doesn't work any more.

So, let us design a second clause that takes care of sentences like ``John loves Mary'' of the form (noun+(verb+object)). Here it is:

insertArgs(N+(V+O),V) :-
        compose(V,_,[N,O]).

?- Question!

Try this call: s(Sem,[john,loves,mary],[]), insertArgs(Sem,Inserted). Explain in your own words how the above clause of insertArgs/2 works. Add lexical rules for a few other words (along the examples) to the DCG and play a bit with the program on your own computer:

1. Download firstAttempt.pl and extend the DCG.

2. Start Prolog and consult the file:

   ?- [firstAttempt].

3. Parse a sentence or some other phrase (you have to give it as a list of atoms) and post-process the resulting + term:

   ?- s(Sem,[peter,sleeps],[]), insertArgs(Sem,Inserted).

   (Assuming you've added lexical rules for peter and sleeps).