2.1.3 Representing Complex Formulae

Boolean combinations of simple formulae.

Next for Boolean combinations of simple formulae. The symbols

Connectives as Operators.

&       v       >       ~

will be used to represent the connectives 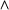, , 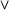, 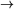and respectively.

comsemOperators.pl: View Download

The following Prolog code from comsemOperators.pl ensures that these connectives have their usual precedences:

:- op(800,yfx,&).         % conjunction

:- op(850,yfx,v).         % disjunction

:- op(900,yfx,>).         % implication

:- op(750, fy,~).         % negation

?- Question!

Have a look at Learn Prolog Now! if you are unsure about what this code means. To test your understanding: How would the following look in fully bracketed version?

• love(john, mary) & love(mary, john) > hate(peter,john)

• love(john, mary) & ~ love(mary, john) > hate(john.peter)

• ~ love(mary, john) v love(peter,mary) & love(john, mary) > hate(john.peter)

Quantifiers

Finally, we must decide how to represent the quantifiers. Take for example the first order formula 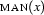. man(x) is its representation as a Prolog term. Now 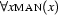will be represented as

forall(x,man(x))

and 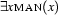will be represented as

exists(x,man(x))

Remember that the fact fovar(x) has to be in the database because we want x to stand for a variable.

Exercise 2.2, Exercise 2.3 and Exercise 2.4 deal with checking the well-formedness of formulae in Prolog representation, and with the relation between vocabularies and formulae.