10.3 Running First-Order Tableaux

We now provide driver predicates and give you a listing of all files you need in order to experiment with first-order theorem proving or model generation.

fo.pl: View Download

We now provide driver predicates and give you a listing of all files you need in order to experiment with first-order theorem proving or model generation. The driver predicates (found in fo.pl) aren't very exciting:

modGen(Formula,Model,Qdepth) :-
        naonly(Formula,ConvFormula),
        tabl(true(ConvFormula),[],Model,[],[],Qdepth).

modGen(_,_,_) :-  
        format("~nNo model found!~n",[]).

We have added a clause for existentially quantified formulae to naonly/2 that re-writes formulae of the form 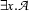into the equivalent 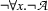. The call to tabl/6 requires the outgoing quantifier list to be empty. We argued in the last section that this is important for the control of the quantifier instantiations.

Try it!

modGenWrite/3 is a version of modGen/3 producing formatted output. Try it out: modGenWrite((forall(x,man(x)>(exists(y,man(y) & father(y,x)))) & man(john)),M,10). In this example, you can see that we really have to control the application of the quantifiers. For this input, our system might generate fathers till the end of time. Only our limited Qdepth ensures that it halts as soon as it has generated 10 fathers.

The driver for theorem proving (also found in fo.pl) is even simpler:

theorem(Formula,Qdepth) :-
        naonly(Formula,ConvFormula),
        \+ tabl(false(ConvFormula),[],_,[],[],Qdepth).

You can test it like this: theorem((forall(x,man(x)v~man(x))),10).

Modules