10.2.4 Universal Rule: The Prolog Clause
The treatment of universal quantification in the implementation.
We are now prepared to look at the implementation of the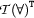 
clause of tabl/6. This clause generates the first instantiation of a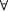 
-quantifier-scope and puts the quantifier on the quants-list. In a minute, we will turn to the more subtle matter of when and how to do the subsequent instantiations with other individuals.
tabl(true(forall(X,Scope)),InBranch,OutBranch,QuantsIn,QuantsOut,Qdepth) :-
!,hbaseList(InBranch,HBase),
member(Ind,HBase),
subst([X:Ind],Scope,NewInstantiation),
tabl(true(NewInstantiation),InBranch,OutBranch,[(forall(X,Scope),[Ind])|QuantsIn],QuantsOut,Qdepth).
First, hbaseList/2 (from comsemLib.pl) generates the current Herbrand base from the current model. Then member/2 picks some individual from the Herbrand base and subst/3 generates the first (and therefore trivially new) instantiation of the quantifier's scope. For example, if our formula at hand is true(forall(x,walk(x))) and the current model (InBranch) is [true(woman(mary)),true(man(john))], HBase will be instantiated to [mary,john]. The new instantiation will then be true(walk(mary)).
In the recursive call to tabl/6, the QuantsIn-list is extended by a tuple of the form (forall(X,Scope),[Ind]). In our example, this is the tuple (forall(x,walk(x)),[mary]). So, if we want to instantiate the quantifier again later on, we know that we have already instantiated it once before, namely with mary.
Who is *?
By definition, the universe of a model must not be empty. This means we must never have an empty Herbrand base. In order to avoid this, hbaseList/2 is designed such that it never returns an empty list. If there is no constant on the branch so far (i.e. in the ``developing'' model), we put in a joker individual * instead. One result of this is that we always have a constant for the first instantiation of a quantifier.