Exercise 6.1

Make sure that the clause of combine/2 given in Section ``'' really corresponds to the tree representation given there: Print out the tree and try to decorate its nodes with all respective Prolog variables for the nodes.

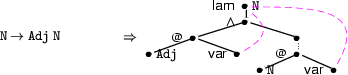
Exercise 6.2

1. Write down the -expression that corresponds to the graph given in Section ``Example: ``A woman walks'' ''. Reduce this -expression to a first order formula.

   Hint: the right half translates into . In the left half, there are two -nodes. Each translates into where is a new variable. The existential quantifier has to be treated likewise. -nodes translate into the variables bound by their binder.

2. Look at our implementation of the predicate translate/4 (see cllsLib.pl) that translates solved constraints into -terms. Explain how the bindings are handled!

   cllsLib.pl: View Download

   This predicate converts solved constraints directly to -terms. Note that we only compute one (minmal) solution for one solved form. But as we have discussed solved forms stand for classes of solutions. Which clause of our predicate would we have to change in order to compute non-minimal solutions?

Exercise 6.3

Test whether you understand the semantic macro for the indefinite determiner a. The "naked" tree given in the figure in Section ``Macros for the Determiners'' on the right is already decorated with the PROLOG variables from the semantic macro detSem(indef,...). Print out this tree or draw it on a piece of paper. Go through the semantic macro and add the node labels and the binding edges to the tree.

Exercise 6.4

cllsLib.pl: View Download

Look at the two clauses of mergeUSR/2 (cllsLib.pl) and make sure that in the resulting constraint, the root node of the leftmost input constraint really ends up in front of all other nodes. Remember that we always interpret the first node of a constraint as its root node. This means we have to be able to formulate our calls of mergeUSR/2 such that we can determine which node will finally be the root node.

Design a test call

  
USR_A = usr([nodeA1,nodeA2,...],[nodeA1:lA1,...]...),
USR_B = usr(nodeB1,...),
USR_C = usr(...),
mergeUSR(merge(merge(USR_A,USR_B),USR_C),Result).

to practically test this.

Exercise 6.5

Add a treatment of adjectives to the implementation of clls. The semantic macro for an adjective is a USR for a simple labeled node. Procede as follows: First, complete the semantic macro adjSem(_,_) for adjectives (to be found at the bottom of clls.pl). Second, add a clause of combine to clls.pl according to the following scheme.

Exercise 6.6

solveConstraint.pl: View Download

The implementation of liftDominanceConstraints/2 we presented immediately removes the old, lifted dominance edge with select/3 (see Section 6.3.4).

There is a problem if we use member/2 instead of select/3? Try it out! Why does this problem occur? Can you think of an elegant solution to it?

Hint: look what predicates we've already got for cleaning up constraints!

Exercise 6.7

[optional]

clls.pl: View Download

In the implementation of clls we presented, the meaning of a determiner as given in the semantic macros is a relatively complex -structure (tree). It represents e.g. the -term in the case of the universal quantifier. The only part of such trees that is relevant for the semantics construction process is its root node. The rest of the tree remains stable during the whole construction process: There is no place inside these trees where further material can be inserted. To enhance the readability of the underspecified structures, one can for example represent the meaning of an universal quantifier as a node labeled every during the semantics construction process. Then, before the final -reduction is done, these abbreviations can be be expanded into the well-known -terms like .

Try to change the implementation of clls accordingly. You may proceed as follows. First, replace the entries of the determiners in the semantic macros by simple labeled nodes (like the entries of nouns for example). Then, build a PROLOG module ExpandQuantifiers that exports a predicate ExpandQuantifiersList/2. This predicate should expand a list of -terms containing abbreviations like [every@man@lambda(A,walk@A)] into the list [lambda(P, lambda(Q, exists(X,(P@X)&(Q@X))))@man@lambda(A,walk@A)] Finally, integrate the predicate ExpandQuantifiersList/2 into the predicate clls.

Hint: use the predicate compose/3 (comsemLib.pl) to decompose terms like every@man@lambda(A,walk@A) .

Exercise 6.8

[Mid-Term Project]

solveConstraint.pl: View Download

Our implementation of solve/2 is a straightforward implementation of the enumeration algorithm. It is an example of imperative programming. For example, the solutions of two distributed constraints are computed at once and then they are solved recursively. Finally, the results are appended.

The same could have been achieved in a more declarative fashion with backtracking and two clauses of distribute. Reimplement the predicate in a more declarative manner!

Hint: use Prolog search (like bagof) to enumerate all solutions.