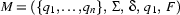Exercise 3.1

What language does the regular expression describe? Sketch the step-by-setp construction of an automaton along the lines of our proof in Section 3.1.5. To make this task a bit less cumbersome, here are some simplifications that you can make:

• You don't have to treat , , and as complex, that is you can read each of them as a whole word over one edge.

• You don't have to give names to the states. Just draw empty circles.

• The solution you hand in needn't contain all intermediate step. That means you can re-use for the next one what you've drawn in one step and don't have to copy over and over.

Exercise 3.2

Now draw an automaton for as you would normally do it (that is, don't stick to the proof in Section 3.1.5). Compare!

Exercise 3.3

In Section 3.1.5 we looked at one direction of the equivalence between regular expressions and FSAs. We showed that every language that can be characterized by a regular expression is also accepted by some FSA. Now let's look at the other direction and prove that for every FSA there is a regular expression that characterizes the same language.

Let

be a deterministic FSA, and be the language accepted by it. We are going to show that there is also a regular expression for .

Before we begin, let's define the following notion: are those strings that reads when it goes from to without passing through a state numbered higher than (by passing through, we mean entering and leaving again). So and may have numbers greater than . We will use to ``zoom'' in and out of our automaton, determining that only a part of it may be used.

Now our induction will be over . Starting from single states we successively allow ourselves to use larger parts of our automaton. We have to show that (given any choice of ):

Basis

There is a regular expression that characterizes . This is the language of all strings that take from to without going through any state numbered higher than 0 (that is infact, without going through any state at all).

Induction

There is a regular expression for , given that there is one for for any choice of .

Give proofs for basis and induction! To prove the basis, you can of course simply enumerate as a disjunction all the words that can be read in in one step from to . For the inductive step, think about the following: If a word can be read from to in without going through any state higher than , it can always be split into a sequence of parts none of which takes through a state higher than (in the sense of entering and leaving). How can this be done?

Exercise 3.4

Add a ``pretty-print'' operation (you can call it pr) to the operations defined in Section 3.3. It should use the backbone of the scan/1-predicate to crawl along an automaton and print out messages with information about any state it visits and about any edge it passes.

For instance loading haha.pl and then calling scan(pr(a1)). should result in output like the following:

automaton a1:
 
initial state 1
 
from 1 to 2 over h
etc...
 
final state 4
 
yes

Hint: One way of producing formated output in Prolog is using the format/2 predicate. The first argument of format/2 is a string (i.e. something that's enclosed between double quotes). This string may contain one or more placeholders. The second argument is a list of things to be printed instead of these placeholders.

For instance the call

format("My ~w has ~w legs.~n My ~w has ~w legs.~n", [dog, 4, sister, 2]).

produces the following output:

My dog has 4 legs.
My sister has 2 legs.
 
yes

The string given as first argument in this call contains the placeholder symbol ~w four times. These four placeholders are then replaced by the items on the list in the order in which they occur. Furthermore the strings contains the special symbol ~n twice. This is printed as a linebreak.

There are lots of other ways of using the format-predicate, for instance with other kinds of placeholders and for file output. You will find them documented with most Prolog implementations. For this exercise, ~w and ~n should do.

Exercise 3.5

In Section 3.2.2 we saw how to build complement automata, that is how to make an automaton that accepts some language into an automaton that accepts .

The method we discussed there works for FSAs that are complete, deterministic and -free. We did not implement a complementation-operation in our Prolog system in Section 3.3 because we did not want to bother with establishing these properties.

Add a complementation-operation comp to the implemetation. Your operation may simply assume that the input FSA is complete, deterministic and -free. The file deterministic.pl contains a complete, deterministic (and of course -free) version of our very first laughing machine. Use this file to test you implementation.