3.2.3 The ``Pumping Lemma''

The Puming Lemma allows one to tell that a language is not regular.

We will now look at another interesting property of regular languages that often allows us to tell that a language is not regular. We will first illustrate the basic idea. Consider our simple ``laughing machine'' (already well known from Section 1.1.1):

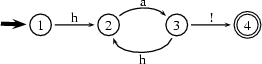
The automaton has four states. This means that the only word it can accept without visiting any state more than once is the three-symbol word ha!. All other words from the ``laughing language'' require it to visit some state(s) more than once. We can easily see from the diagram that these are the states 2 and 3. They will be visited twice when accepting haha!, three times when accepting hahaha!, etc.

This observation can be generalized: Let 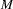be an automaton with states that accepts a language . Then for any word 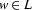that consists of or more symbols, there must be at least one state in 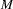that is visited more than once when is processed. Now if a state (or sequence of states) in a FSA can be visited more than once, it can be visited any number of times. This is so becaues such a FSA must contain a loop, and we are free to go through it as often as we like. Let's suppose 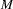reads the word while going through the loop. So we know that can be split in parts as follows: 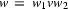. But this means that, by looping on , 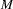will as well accept 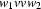, , 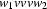etc.

Take for instance our laughing machine above. We had to go through 2 and 3 twice to accept haha!, using the loop from 2 to 3 and back. On our way through this loop we read ha (the second occurence, to be precise). And we can go through this loop any number of times. Looping like this we accept hahaha!, hahahaha! etc.

The above considerations lead to the following lemma, known as the ``Pumping Lemma'', because it says that we can ``pump'' up words in regular languages under certain conditions. (By 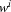we mean the result of repeating i-times; 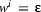. By 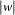is the length of .):

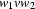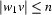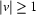Let be a regular set. There is a constant such that if is any word that is in and is of length greater , then we can split in parts with and , and 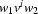is in , too for all 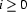. Moreover, we know that is no greater than the number of states in the smallest FSA accepting .

The main use of the pumping lemma is in showing that a given language is not regular. Consider for instance the language 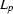of all palindromes (``symmetrical'' words that are the same whether you read them forward or backwards) that can be formed over some alphabet containing more than one symbol (say 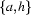). 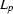contains words of any finite length. Now if 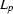was regular, all of its words exceding a certain length could be ``pumped'' on, and all the resulting words would also be in 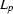. In particular, this would be

Now take the palindrome 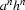. The ``Pumping Lemma'' states that there is some substring within the first symbols, thus a substring consisting entirely of as, that we should be allowed to repeat arbitrarily often without leaving 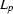. Yet obviously any such repetition of as would destroy the symmmetry in and the resulting word would no longer be a palindrome.