10.5.1 Representations

First, we have to decide how to represent -expressions in Prolog

First, we have to decide how to represent 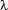-expressions in Prolog. As in the case of representing first-order formulas, we will use Prolog terms that resemble the expressions they represent as closely as possible. For abstractions, something as simple as the following will do:

lambda(x,F)

Secondly, we have to decide how to represent application. Let's simply transplant our @-notation to Prolog by defining @ as an infix operator:

 :- op(950,yfx,@).         % application

That is, we shall introduce a new Prolog operator @ to explicitly mark where functional application is to take place: the notation F@A will mean ``apply function F to argument A''. We will build up our representations using these explicit markings, and then carry out 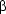-conversion when all the required information is to hand.