3.2.9 Sidetrack: Constraint Graphs - The True Story

In the example, we have been able to cover the complete -structure with the fragments in the constraint graph. This need not be the case in general: As the fragments only have to be embedded into the -structure, it is possible that the latter contains some material not mentioned in the graph.

More Flexibility

This makes sense from a computational point of view, considering that constraint graphs are provably harder to deal with if solutions are not to contain additional material. From a linguistic point of view, one can take the idea behind underspecification even further, using the same formalism to deal not only with scope ambiguities, but also with cases where, for example, a speech recognizer has failed to recognize certain parts of the input. In such cases, we want flexibility to add more material to a solution - in a controlled way, of course.

Embedding vs. Configuring

We will ignore this point here and assume that we'll never need to invent any additional material to solve the constraint graphs we get for scope ambiguities. So we can think of the process of solving a constraint as configuring the fragments into a bigger tree. It can be shown empirically that the distinction between configuring and embedding makes no difference in practice [FKNT04].

The difference between embedding and configuring may become clearer with an example given. Consider the following constraint graph:

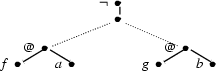
Additional material...

This constraint graph trivially has a solution. It starts with the topmost fragment. Then we put an arbitrary label (like @) at the leaf of this fragment and say that this node should have two children. The left child should be the root of the lower left fragment, while the other child should be the root of the lower right one:

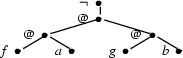
...or not?

But if we insist that we have to configure the fragments, without adding any new material, the answer is not so clear. Only if one of the two lower fragments had an unlabeled leaf, it would indeed be possible to configure them by attaching the other fragment to this leaf. Otherwise, it is impossible to configure them; this is the case in the example. Of course, it might take us a long time to figure out that we have plugged fragments together in the wrong order if the graph is larger. That's why computation becomes harder when we restrict ourselves to configuration instead of embedding.

Although we have presented constraint graphs a bit informally here, they can be given a very precise meaning as a shorthand notation for logical formulas, which then are called normal dominance constraints . In fact, if you look at the literature on dominance constraints [EKN01], you'll find that the logical formulas are always the first concept to be defined, and the constraint graphs are then derived from them.