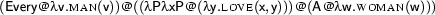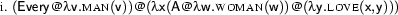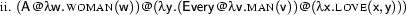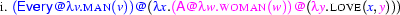5.1.2 Scope Ambiguities and Montague Semantics

Montague's treatment of scope ambiguities.

Using our Implementation

Now let's see what Montague Semantics has to say about this. In Exercise 4.5, we asked you to test our implementation of -calculus and to try to find sentences the approach does not handle properly.

Maybe you've come up with sentences containing scope ambiguities like ``Every man loves a woman''. We have just seen that this sentence has two readings, but our implemented system only gets one of them:

?- lambda.
 
> every man loves a woman.
 
1 forall(A,man(A)>exists(B,woman(B)& love(A,B)))
 
yes

If you like to, reproduce this result at your computer: lambda([every,man,loves,a,woman],Sem) . This is a correct representation of one of the possible meanings of the sentence - namely the one where the quantifier of the object-NP occurs inside the scope of the quantifier of the subject-NP. We say that the quantifier of the object-NP has narrow scope while the quantifier of the subject-NP has wide scope. But the other reading is not generated here! This means our algorithm doesn't represent the linguistic reality correctly.

What's the problem?

This is because our approach so far constructs the semantics deterministically from the syntactic analysis. Our implementation simply isn't yet able to compute two different meanings for a syntactically unambiguous sentence. The reason why we only get the reading with wide scope for the subject is because in the semantic construction process, the verb semantics is first combined with the object semantics, then with that of the subject. And given the order of the -prefixes in our semantic representations, this eventually transports the object semantics inside the subject's scope.

A Closer Look

To understand why our algorithm produces the reading it does (and not the other alternative), let us have a look at the order of applications in the semantic representation as it is before we start 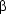-reducing. To be able to see the order of applications more clearly, we abbreviate the representations for the determiners. E.g. we write 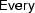instead of 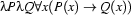. We will of course have to expand those abbreviations at some point when we want to perform 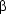-reduction.

After 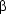-reducing the VP once, things look a little nicer:

The resulting expression is an application. The universal quantifier occurs in the functor (the translation of the subject NP), and the existential quantifier occurs in the argument (corresponding to the VP). The scope relations in the 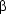-reduced result reflect the structure in this application.

An Idea for a Solution

With some imagination we can already guess what an algorithm would have to do in order to produce the second reading we've seen above (where the subject-NP has narrow scope): It would somehow have to move the 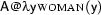part in front of the 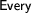. Something like the following expression would do: