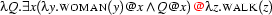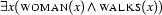3.4.3 Using Lambdas
The use of
-calculus for semantic construction.
Fine, now we have a tool for juggling around with missing information in incomplete first order formulae. But does it really solve our problems? Does it help us when we want to construct a semantic representation for a sentence compositionally?
Let's return to the sentence ``A woman walks''. According to our grammar, a determiner and a common noun can combine to form a noun phrase. Our semantic analysis couldn't be simpler: we will associate the NP node with the functional application that has the determiner representation as functor and the noun representation as argument (we mark this application by inserting an @ between functor and argument).
Building a structured application...
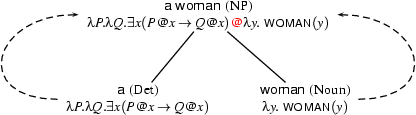
Let's carry on with the analysis of the sentence. We now have to incorporate the intransitive verb ``walks''. We assign it the representation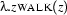 
. The following tree shows the final representation we obtain for the complete sentence:
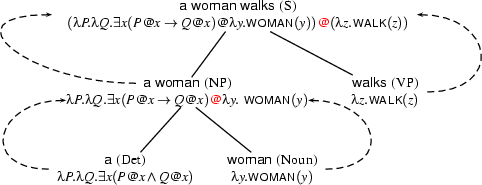
The S node is associated with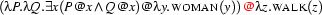 
. We obtain this representation by a procedure analogous to that just performed at the NP node. We associate the S node with the application that has the NP representation just obtained as functor, and the VP representation as argument.
Up to now it may seem as if we haven't gained much. The representation at the S-node has the same internal structure as
(exists(_,_&_)+woman(_))+walks(_) produced by our first attempt for the same sentence. But now comes the time that the -prefixes in our new representations really help us solve a problem.
...and reducing it.
Instead of hand-tailoring some specially dedicated post-processing method, we will simply 
-reduce the expression we find at the S node. Let's see what happens. We must follow its (bracketed) structure when we perform -reduction, so we start with reducing the application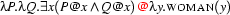 
. We have to replace 
by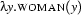 
, and drop the 
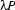prefix. The whole representation then looks as follows:
Let's go on. This time we have two applications that can be reduced. We decide to get rid of the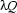 
. Replacing 
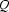by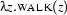 
we get:
Again we have the choice where to go on -reducing, but this time it should be clear that our choice doesn't make any difference for the final result (in fact it never does. This property of -calculus is called confluence ). Thus let's -reduce twice. We have to replace both 
and 
by 
. Doing so finally gives us the desired:
?- Question!
Look at the representations 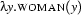and 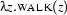again. It may seem strange at first sight that we give semantic representations for intransitive verbs that are structurally like the ones for common nouns. Yet from the point of view of logics, this is the obvious thing to do. Why?