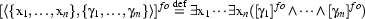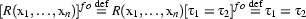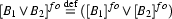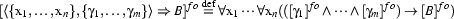11.3.5 Translations to First-Order Logic

It is possible to translate the representations of DRT into first-order logic syntax.

Apart from giving a direct semantics for DRSs (as we formulated for the embedding semantics and for the context change potential semantics), it should be noted that it is also possible to translate the representations of DRT into first-order logic syntax. Once we are able to do that, we can just use the interpretation methods for first-order logic to give a semantics to DRSs.

The translation from DRSs to first-order logic is surprisingly simple, and can be accomplished by defining a translation function (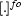, from DRS or DRS-conditions to first-order formulas) as follows.

This maps the discourse referents to existentially quantified variables, and recursively translates the conditions. The remaining clauses deal with the DRS-conditions. Basic conditions simply map to themselves, viewed as first-order atomic formulas:

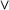Moreover, complex conditions formed using and are also straightforwardly handled; we simply push the translation function in over the connective, leaving the connective unchanged:

Finally, complex conditions formed using 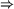are translated as follows.

Translations as above are known to preserve the logical meaning. That is, given a model 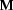and an assignment 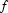, it can be shown that a DRS B is true in 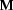with respect to 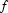iff 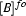is satisfied in 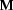with respect to assignment .

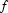In the next section we will implement this translation in Prolog, and implement a way of building DRSs for English expressions in a systematic way.