10.1.3 The Existential Rule

Introducing witnesses for existential quantifications.

What does an existential (respectively the equivalent negative universal) statement tell us? Intuitively, if we know that ``Somebody smokes'' (respectively that ``It's not the case that everybody doesn't smoke''), then all we know is that there is somebody who smokes, but we have no clue who it is. It may be someone we know of (say John or Bill), but it may just as well be someone we don't know yet. Therefore, the existential statement does not warrant the conclusions ``John smokes'' or ``Bill smokes'' - claiming any of these we would commit ourselves too much. John and Bill may both be non-smokers and ``Somebody smokes'' still be true. But what we can do is give the unknown smoker a name that we invent only for him (we might call him ``N.N.''). So we can be sure that we don't say anything wrong about someone we already know of; we can let Bill and John remain non-smokers in a world where nevertheless somebody smokes. This idea is formalized in the following rule:

Existential Rule

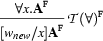
Introducing a Witness

We take the scope of a negative universal quantification and substitute a brand new constant 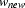for the quantified variable. The new constant is also called a witness or skolem constant . It is like the new name that we decided to invent for the smoker in our example. Because that witness constant is not contained in any of the formulae on the tableaux so far, the tableaux cannot close on a direct contradiction between any of these formulae and the coclusion of the 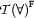-rule. Let's look at an example:

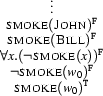
In the second but last line, we have invented the witness 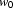for the scope of the existential quantification. We have generated a model in which John and Bill do not smoke, but nevertheless somebody (whom we call 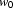) smokes.

The fact that our new constant cannot immediately be involved in closing the tableau does not imply that it cannot ever be involved in closing it. Contradictions may arise with consequences of universally quantified formulae, because once a witness constant has become available, it can be used with the 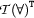-rule. Let us look at a tableaux where this happens. The formula 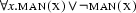is obviously valid. It is equivalent to 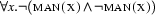(``it is not the case that there exists a man that isn't a man.''), for which we now give a tableaux proof:

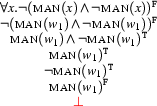
In the first step, we again invent a witness (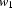, ``the man that is no man'') for the scope of the existential quantification. We then derive a contradiction for this witness, about which we know nothing else and did not make any further assumptions. Yet of course we could have derived that contradiction with any other choice of constant instead of 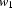, too. So the fact that we could derive it does not mean that our policy of inventing new constants has failed. On the contrary we have to be able to derive such contradictions involving universal quantification for our calculus to be complete.