10.1.1 Why First-Order Inference?

Motivation of first order inference.

As a logician, it's just a normal thing to ask if it's possible to extend what you've done for propositional logic to first-order logic. But apart from this there're especially good reasons to do so if you're interested in computational semantics: As a matter of fact, natural language contains lots of quantified NPs, which are formalized using quantifiers. Thus if we want to be able to infer from such sentences, we must have a treatment of quantifiers in our calculus.

Quantification in natural language...

In PLNQ we could only formulate (and therefore only infer from) particular statements about named entities. Up to now we could infer from the premisses

• ``Mary sleeps.'' and ``If Mary sleeps then Mary snores.''

that Mary snores. But we could for instance neither express the generalization ``Every man snores.'', nor could we infer from this and ``John is a man.'' that John snores. In order to express the premiss of this argument, we have to let quantifiers into PLNQ, thus arriving at the language of full first-order logic. And in parallel our calculus has to be able to work with them in order to validate such arguments.

...and in world knowledge

But the omnipresence of quantification in natural language is not the only reason why we want to have first order inference. We are particularily interested in deriving the consequences that follow from our world knowledge together with some particular natural language sentence that's been uttered. Remember we argued above that it is a great advantage of our tableaux based model generation method that we can readily infer from any kind of background knowledge by simply including it on the (initial) tableaux. But world knowledge characteristically consists of generalizations, such as ``Every cat is furry.'' or ``Every human has a father.''. So we need quantified formulae to formalize world knowledge (such as 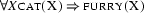and 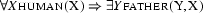). This means that inference becomes essentially first-order if we take world knowledge into account.

In fact both of the above arguments are also small lies. There's a lot of teritorry that lies between propositional and first-order logic, and it may well be that we don't really need full first-order logic and inference for the described tasks. There's a lot of research going on that tries to answer two questions:

• How much of first order logic do we need in order to formalize exactly those cases of quantification that really occur in natural language and world knowledge, no more and no less?

• How can we use clever formalizations and representations to support just the kinds of inferences we need, without bothering about the full complexities of first-order inference.

We will see in this chapter where we get using full first order logic. One thing we'll learn this way is to appreciate why it is so important to study what's in between propositional and first-order.