7.2.1 Tableaux for Theorem Proving

Introduction of tableaux.

Tableaux are data structures used in refutation-based procedures for automated theorem proving. Tableaux are trees labeled with formulae. They are constructed starting from a single (root) node, which is labeled with an input formula. From this node, a tree is constructed by recursively decomposing complex formulae along the lines of their logical connectives. Finally, the literals on each branch of this tree tell us what has to be true (and what has to be false) in some class of models of the input formula, and (this is an important point) all branches of the tableaux taken together represent all models of the input formula.

Closed Tableaux: No Model

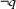If a branch of a tableaux contains a contradiction (e.g. the literals and ), this branch is called closed . Branches that are not closed are called open . No models correspond to a closed branch (because two contradictory literals cannot be true in any model). So the nice thing is that if all branches of a tableaux are closed, we're sure that there is no model at all for its input formula. This is a direct consequence of the fact that a tableaux enumerates all models of the input formula.

Here's how we can make use of this fact in theorem proving: When trying to prove that a formula is a theorem, we want to show that the formula is true in all models. But we needn't do that directly. As you know, it is a common technique in mathematics to prove something by showing that its negation cannot be true. This is exactly how tableaux proofs work: If we want to show that a formula is a theorem, we prove that there is no way to make it false. So in order show that a given input formula is true in all models, we will show that there is no model for its negation.

Constructing a Tableaux Proof

Now what does all of this mean in terms of tableaux? We start with the negation of our suspected theorem, and construct a tableaux by decomposing it into subformulas step by step. To prove that it really is a theorem if we have to arrive at a closed tableaux at some point.

But how exactly do we construct the tableaux? Here's an example. Let's try to show that the formula 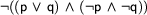is a theorem. As explained above, we start with only a single node containing the negation of this initial formula. Instead of using the sign here, we indicate the top level negation that we've added to our input formula by signing the formula with an :

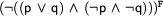
Signed Formulae

All formulae in our tableaux calculus will be signed in that way as either or . The signs are best thought of as instructions that tell us that we have to make a formula true or false, respectively. Of course these signs were not covered by our original definitions in Chapter 1. Extending the syntax accordingly, it makes sense to adjust the definition of ``literal'': Literals are signed atomic formulae. This means that (in contrast to our old definition) literals never have any connectives; we will no longer regard formulae with a negation symbol () as literals, even if the scope of the negation is atomic.

Next let's see how we can make our input formula false (following its sign). It has a negation as its main connective. Thus we know that it is false iff its unnegated version is true. So, we add a node (we give it number 1 here) to our tableaux with the respective unnegated formula:

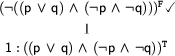
Conjunctive Expansion

We mark formulae that we have already expanded by 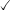. Now, look at the formula at node 1. The sign tells us that we have to make this formula true. We can do so by making both of its conjuncts true. So, we add two new nodes to our tableaux (we call this a conjunctive expansion of a formula respectively a branch):

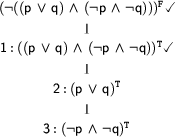
Up to now, we have found out that we make our input formula false iff we make both (less complex) formulae 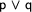and 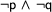true. You might already see that this is not possible, but a computer certainly won't. So let us further expand these formulae!