5.2.9 Sidetrack: Constraint Graphs - The True Story

It is possible that a -structure contains some material not mentioned in the graph.

In the example, we have been able to cover the complete -structure with the fragments in the constraint graph. This need not be the case in general: As the fragments only have to be embedded into the -structure, it is possible that the latter contains some material not mentioned in the graph.

More Flexibility

This makes sense from a computational point of view, considering that constraint graphs are provably harder to deal with if solutions are not to contain additional material. From a linguistic point of view, one can take the idea behind underspecification even further, using the same formalism to deal not only with scope ambiguities, but also with cases where, for example, a speech recognizer has failed to recognize certain parts of the input. In such cases, we want flexibility to add more material to a solution - in a controlled way, of course.

Embedding vs. Arranging

Here we will be ignoring this point, and eventually it will turn out that we'll never need to invent any additional material to solve the constraint graphs we get for scope ambiguities anyway. It is safe to think of the process of solving a constraint as arranging the fragments into a bigger tree.

The difference between embedding and arranging may become clearer with an example given. Consider the following constraint graph:

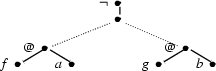
Additional material...

This constraint graph trivially has a solution. It starts with the topmost fragment. Then we put an arbitrary label (like @) at the leaf of this fragment and say that this node should have two children. The left child should be the root of the lower left fragment, while the other child should be the root of the lower right one:

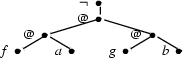
...or not?

But if we insist that we have to arrange the fragments, without adding any new material, the answer is not so clear. Only if one of the two lower fragments had an unlabeled leaf, it would indeed be possible to arrange them by attaching the other fragment to this leaf. Otherwise, it is impossible to arrange them; this is the case in the example. If we take an example of larger scale, of course, we might be able to start with the arrangement process, but then notice somewhere down the line that we have plugged fragments together in the wrong order. That's why computation becomes much harder when we restrict ourselves to arrangement instead of embedding.

Although we have presented constraint graphs a bit informally here, they can be given a very precise meaning as a shorthand notation for logical formulas, which then are called normal dominance constraint s. In fact, if you look at the literature on dominance constraints, you'll find that the logical formulas are always the first concept to be defined, constraint graphs being then derived from them. If you'd like to know the true true story about constraint graphs, you can ask us for literature on dominance constraints.