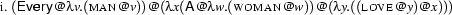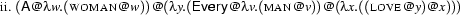5.2.6 Describing Lambda-Structures
Describing
-structures.
There is of course no reason to restrict our new tree notation to formulas of first-order logic. We can just as easily represent -expressions. All we have to do is to generally represent application as a tree with the root symbol @ and subtrees for the functor and the argument, and -abstraction as a tree with the root symbol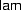 
. Again, we use binding edges to represent variable binding, and thus don't have to give a name to the variable bound by the . We call a tree with binding edges for variable binding a -structure . We can always convert a -expression (or a formula) into a unique -structure. At the same time, every -structure represents a -expression (but not uniquely): All we have to do is invent a new variable name whenever we hit a binder, and then use this name for all bound variables.
Let's look again at the -expressions that lead to the two first order formulae for ``Every man loves a woman''. We have seen these -expressions in Section 5.1.2, and repeat them here:
We have switched again to representations where we abbreviate determiners such as ``every'': 
stands for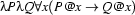 
. In the tree representations that we look at now, we will continue to use such abbreviations, and also abbreviate the simple -expressions and -structures for common nouns. Hence, from now on 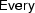abbreviates the -structure for 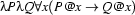, and e.g. 
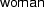stands for the -structure for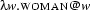 
.
Two lambda-structures...
If we represent the two readings of our example as -structures, we can identify the three formula fragments relevant for the scope ambiguity we're interested in as three tree fragments. We have given them different colours in the picture below.
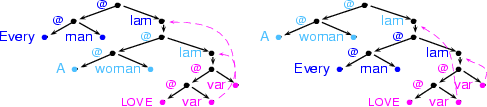
Exercise 5.9
Write down (at least) one of the two readings as a "normal"
. Remember that you have to "invent" a variable for each
by bracketting, e.g.
. Compare the way the transitive verb is combined with its arguments here with the way this was done in
...but only one constraint graph
Now we can represent the information that is common to both readings in the following graph:
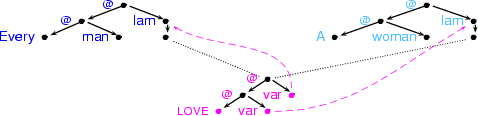
We call a graph as in this picture a constraint graph . A constraint graph is a directed graph that has node labels and three kinds of edges: ordinary solid edges, dotted dominance edge s, and purple arrow binding edge s. It consists of several little tree fragments which are internally connected with solid edges, and connected to other trees with dominance edges. Binding edges generally go from variable nodes to binder nodes.