9.2 The Fundamental Rule
Active arcs are called `active' for a very good reason: They ``actively'' hint at what can be done with them. In particular, we can see at once how to combine them with passive edges to make new edges. The new edges we make may be either passive or active.
Active arcs are called `active' for a very good reason: They ``actively'' hint at what can be done with them. In particular, we can see at once how to combine them with passive edges to make new edges. The new edges we make may be either passive or active.
The fundamental rule for combining a passive edge and an active edge works as follows: Suppose the active edge goes from node 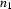 to node
to node 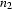 and has category
and has category 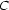 immediately to the right of the dot.
immediately to the right of the dot.
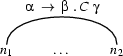
Further, suppose that the passive edge goes from node 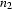 to node
to node 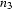 (hence, it starts where the active edge ends) and has category
(hence, it starts where the active edge ends) and has category 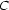 on its left hand side.
on its left hand side.
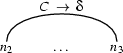
The fundamental rule now allows us to combine these two edges to build a new one that starts in node 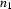 and ends in
and ends in 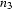 . For the label of that new edge we move the dot in the active edge one category forward.
. For the label of that new edge we move the dot in the active edge one category forward.
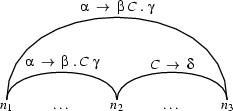
Here are two examples to illustrate the fundamental rule.
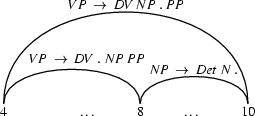
Here we have an active edge (the one on the left) which is looking for a np. And immediately to its right we have an np (note that the edge to the right is passive: that is we really know that there is a np between nodes 8 and 10). Using the fundamental rule, we can combine these edges to build a new edge going from node 4 to node 10. Note, that this new edge is active.
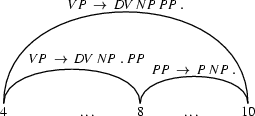
Here we have an active edge (the one on the left) which is looking for a pp. And immediately to the right we have a pp (note that the edge to the right is passive: that is we really know that there is a pp between nodes 8 and 10). Using the fundamental rule, we can combine these edges. Note, that in this case the new edge we have built is passive.